Algorithm CH6 Heapsort

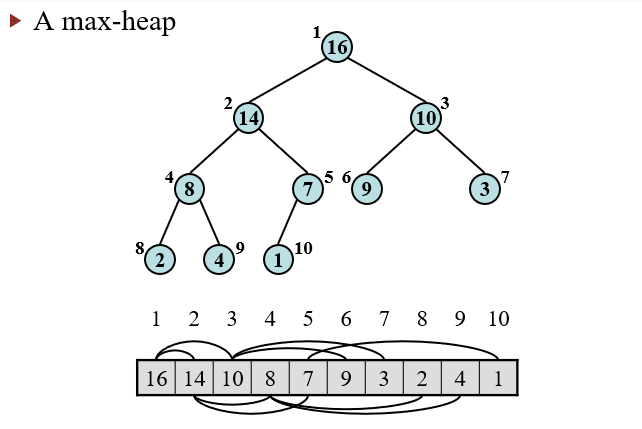
Heap A is a nearly complete binary tree.

• Height of node = # of edges on a longest simple path from the node down to a leaf.
• Height of heap = height of root = (lg n)

A heap can be stores as an array A

• Root of trees is A[1]
• Parent of A[i] = A[ ]
• Left child of A[i] = A[2i]
• Right child of A[i] = A[2i + 1]
• Computing is fast with binary representation implementation

Heap property

• For max-heap (largest element at root), max-heap property: for all nodes i, excluding the root, A[PARENT(i)] A[i].
• For min-heap (smallest element at root), min-heap property: for all nodes i, excluding the root, A[PARENT(i)] A[i].

Maximum element of a max-heap is at the root.

The heapsort algorithm we’ll use max-heaps.

build heap

MAX-HEAPIFY

MAX-HEAPIFY is important for manipulating max-heaps. It is used to maintain the max-heap property.

• Before MAX-HEAPIFY, A[i] may be smaller than its children.
• Assume left and right subtrees of i are max-heaps.
• After MAX-HEAPIFY, subtree rooted at i is a max-heap.

pseudo code

ex.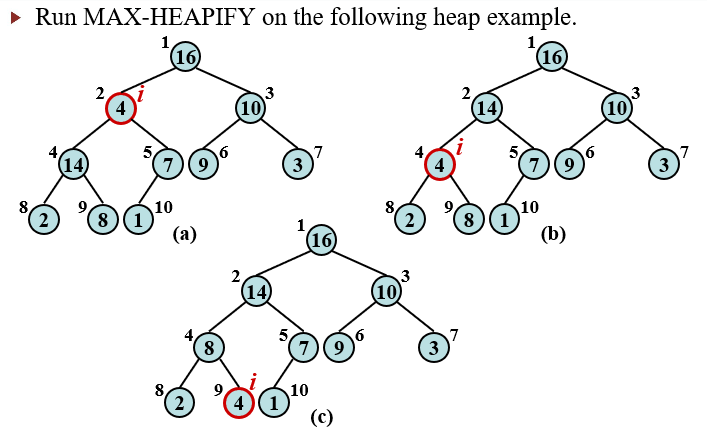

analyse

Time: O(lg n)

Correctness: Heap is almost-complete binary tree, hence must process O(lg n) levels, with constant work at each level (comparing 3 items and maybe swapping 2).

BUILD MAX HEAP

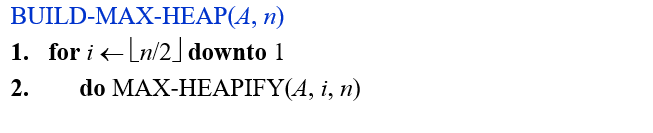
correctness

analyse for build max heap

• 生成函數微分後，乘上x (A.8)

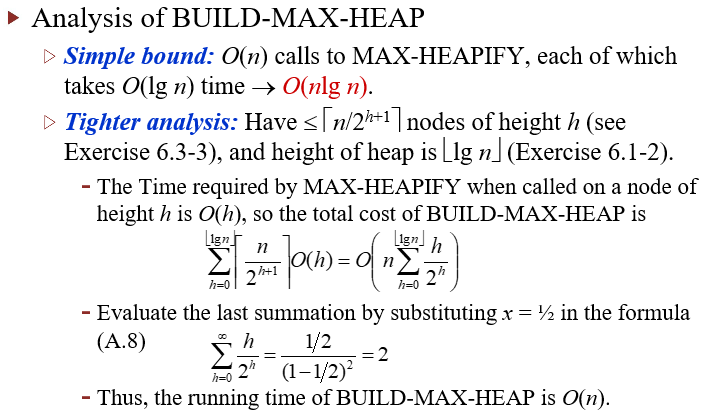
heap sort

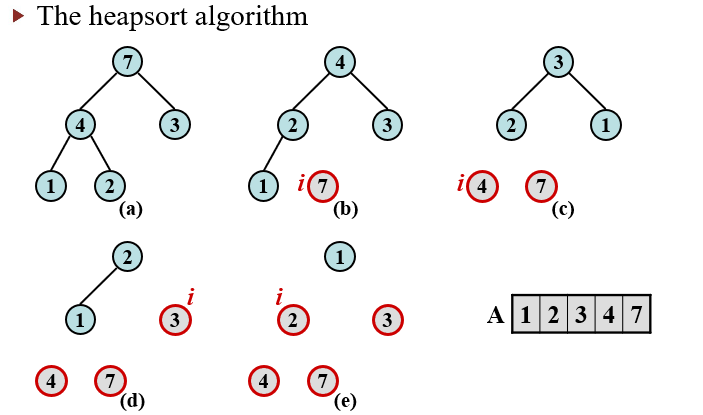
analyse

Analysis of heapsort

• BUILD-MAX-HEAP: O(n)
• for loop: n – 1 times
• Exchange elements: O(1)
• MAX-HEAPIFY: O(lg n)
• Total time: O(nlg n)

Though heapsort is a great algorithm, a well-implemented quicksort usually beats it in practice.

priority queue

Heap implementation of priority queue

• Max-priority queues are implemented with max-heaps. Min-priority queues are implemented with min-heaps similarly.

Max Priority Queues

• Maintains a dynamic set of S of elements.
• Each set element has a key: an associated value.
• Max-priority queue supports dynamic-set operations:
  • INSERT(S, x): inserts element x into set S.
  • MAXIMUM(S): returns elements of S with largest key.
  • EXTRACT-MAX(S): removes and returns element of S with largest key.
  • INCREASE-KEY(S, x, k): increases value of element x’s key to k. Assume k x’s current key value.

Finding the maximum element

• Getting the maximum element is easy: it’s the root.
• HEAP-MAXIMUM(A)
  • return A[1]
  • Time: (1)

Extracting max element

• Given the array A:
  • Make sure heap is not empty
  • Make a copy of the maximum element (the root).
  • Make the last node in the tree the new root.
  • Re-heapify the heap, with one fewer node.
  • Return the copy of the maximum element.

Increasing key value

Given set S, element x and new key value k:

• Make sure k x’s current key.
• Update x’s key value to k.
• Traverse the tree upward comparing x to its parent and swapping keys if necessary, until x’s key in smaller than parent’s key.

Insertion