Algorithm Ch8 Sort in linear time
Algorithm Ch8 Sort in linear time
Lower bounds for sorting
to examine all the input - All sort lower bound are
is lower bound for comparison test
Decision Tree
- Abstration of any comparison sort
- Represents comparison made by
- specific sorting algorithm
- on input of a given size
- Abstract away conotrol & data movement, etc.
- counting only comparison
For insertion sort on 3 elements
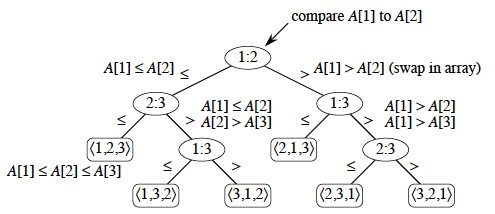 * internal node: indices of array elements from their original pos.
* leaf: permutation of orders that the algorithm determines
* leaf numbers >= n!
* internal node: indices of array elements from their original pos.
* leaf: permutation of orders that the algorithm determines
* leaf numbers >= n!
For any comparison sort
- 1 tree for each n
- view the tree: like algorithm splits in two at each node, base on the inf. is has determined up to that point
- tree models all possible execution tracs
length of the longest path from root to leaf
depends on the algorithm
- Insertion Sort
- Merge Sort
lemma:
any binary tree of height h has <=
- l = # of leaves
- h = height
- l <=
The.
any decision tree that sorts n ele. has height
- Proof.
l >= n!
By lemma,
Take logs, h >= lg(n!)
Use Stirling;s appor.,
$h >= lg(n/e)^n = nlg(n/e) = nlgn - nlge = \Omega(n,lg,n)
Corollary
Heapsort, merge sort are asymptotically optimal comparison sort(最優排序)
Sorting in linear time
Counting sort
Depends on a key assumption: numbers <- {0, 1, …, k}
- Input: A[1…n], where A[j] <- {0, …, k} for all j
- Output: B[1…n], B should be already allocated
- Auxiliary Storage: C[0…k]
pseudo code
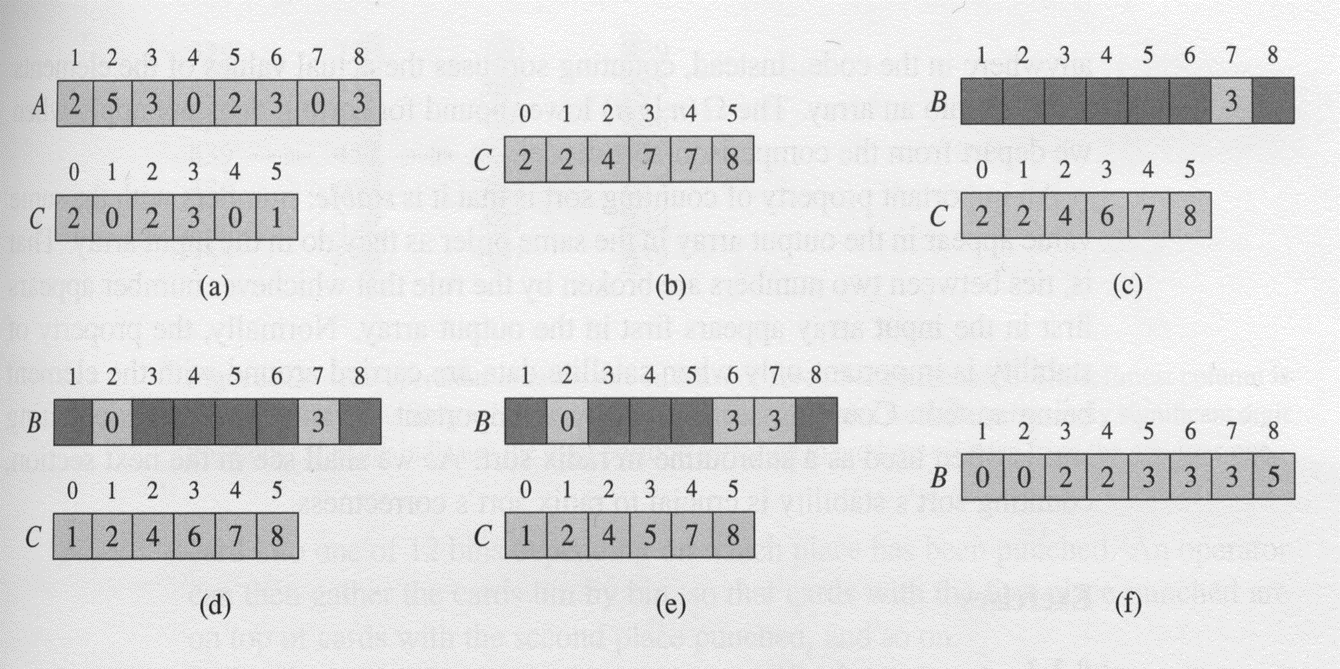
property
- stable because of how the last loop works
- keys with same value appear in same order
Analysis
Is k practical?
- 32-bit? No
- 16-bit? probably not
- 8-bit? Maybe, depending on n
- 4-bit? Probably
- Counting sort used in radix sort
Radix Sort
Sort least significant digits first
To sort d digits:
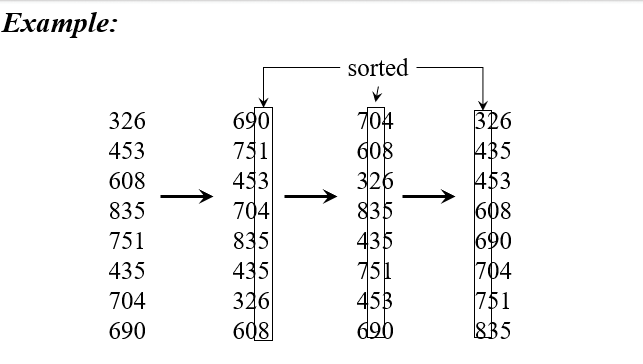
Correctness
Assume digits 1, 2, …, i-1 is already sorted
for
- if two digit are different -> by counting sort
- if … are equal -> count sort is stable, keep order before
It shows why it’s important to use a stable sort for intermediate sort
Analyse
Assume intermediate sort is counting sort
per pass (digit in range 0, …, k) - d pass
total - if k =
, time =
Break digit
- n words
- b bits per word
- Break into r-bit digits. Have d = [b/r]
- Using counting sort, k =
-1 - EX. 32-bit words, 8-bits digits.
- b = 32, r = 8, d = [32/8] = 4
- k =
- 1 = 255
- Time =
How to choose r?
Balance
give us
- if r < lg n
> - n +
do not improve, keep
- if r > lg n
- n +
gets big - Ex. r = 2lg n
= =
- n +
So, to sort
Compare
- 1 million (
) 32-bit int. - Radix sort: ceil(32/20) = 2 passes
- Merge sort/quick sort: lg n = 20 passes
- each passes in radix sort is really 2
- one to take census
- one to move data
why radix can violate ground rule of comparison sort
- using counting sort allows us to gain inf. about key by means other than comparison
- used keys as array indices
Bucket sort
Assume the input is generated by a random process that distributes ee/ uniformly over [0, 1)
Idea:
- Divide [0, 1) into n equal-sized buckets
- Distribute the n input values into the bucket
- sort each bucket
- go through buckets in order, listing ele. in each one
Input: A[1…n], where 0 <= A[i] < 1 for all i
Auxiliary array: B[0…n-1] of linked lists, each list init. empty

Correctness
- Consider A[i], A[j], WLOG, A[i] <= A[j]
- than floor(nA[i]) <= floor(nA[j])
- thus A[i], A[j]
- in the same bucket, by insertion sort => fixes up
- other wise, by concatenation in ordere => fixes up
Analyse
- relies on no buckets getting too many values
- All lines of algo. excpt inserting sort take
altogether(除了插入排序,其他部分總共需要…) - Intuitively, if each bucket gets a constant number of ele., it takes
time to sort each bucket for all bucket
- except each bucket to have few ele., since the average is 1 ele. per bucket
careful Analyse
Def. a RV.
= the number of ele. placd in bucket B[i]
Because insertion sort run in quadratic time, bucket sort time is
- T(n) =
+ $\sum^{n-1}{i=0}O(n{i}^{2})$
Take expectations,
- E[T(n)] = E[
+ $\sum^{n-1}{i=0}O(n{i}^{2}) \Theta(n) \sum^{n-1}{i=0}E(O(n{i}^{2})) \Theta(n) \sum^{n-1}{i=0}O(E(n{i}^{2}))$
Claim,
proof of claim,
Def. indicator RV.
= I{A[j] falls in bucket i} - Pr{A[j] falls in bucket i} = 1/n
=
Then,
and are independent RV. - than
is = =
Therefore
thus
E[T(n)] =
End up
- not a comparison sort
- probabilistic analysis
- different from a randomized algo., where we use randomization to impose a distribution
- With bucket sort, if the input isn’t drawn from a uniform distribution on [0,1), all bets are off (performance-wise, but the algorithm is still correct).