Algorithm Ch9 Medians and Order Statistics

Overview

• ith order statistic: the ith smallest ele. of a set of n ele.
• minimum: the first order statistic(i=1)
• maximum: the nth order statistic(i=n)
• mediam: the halfway point of the set
  • n is odd, median is unique, at i = (n+1)/2
  • n is even, there are two median
    • lower median, at i = n/2
    • upper median, at i = n/2+1
  • we mean lower median when we use the phrase “the median”

The selection problem

Input: A set A of n distinct numbers and a number i, with
Output: The ele. that is larger than exactly i-1 other ele. in A(the ith smallest ele.)

• can be solved in time
  • sort numbers using an -time algo.
    • such as heap sort or merge sort
  • return ith ele. in the sorted array

Minimun and maximum

• can obtain an upper bound of n-1 comparisons fo finding the minimum of a set of n ele.
  • Examine each ele. and keep track of the smallest one
  • the best method

Pseudo code
finds the minimum ele. in array A[1…n]

Simultaneous minimum and maximum

• simple algorithm to find min and max
  • n-1 for minimum, n-1 fo maximum
  • total 2n-2 comparison time

In fact, at most are needed

• compare the ele. of a pair to each other
• compare the larger ele. to the maximum
• compare the smaller ele. to the minimum
• leads to only 3 comparison for every 2 ele.

Init

• if n is even, compare first two ele.
  • assign larger to max
  • smaller to min
• if n is odd, set both min and max to the first ele.

analyse

if n is even, do 1 init. and 3(n-2)/2, that is- 2
if n is odd, 3(n-1)/2 = 3floor()

• In either case, the maximum number of comp. is <= 3floor()

Selection in expected linear time

After the call to RANDOMIZED-PARTITION, the array is partitioned into two subarrays

• A[p..q-1] are all <= A[q]
• A[q+1…r] are all > A[q]
• pivot ele. A[q]

the pivot ele. is kth ele. of subarray A[p…q], where k=p-q+1

• If the pivot is the ith smallest ele. return A[q]
• otherwise
  • i<k, subarray is A[p..q-1], wants the ith smallest ele.
  • i>k, subarray is A[q+1…r], wants the (i-k)th smallest ele.

Analysis

Worst-case running time:

• always recurse on a subarray that is only 1 ele. smaller than previous

Expexted running time: RANDOMIZED-SELECT works well on avearge

• a RV. T(n) to obtain E[T(n)] as follow

Pf.

For k=1,2,…,n, define indicator RV. = I{subarray A[p…q] has exactly k ele.}

Since Pr{subarray A[p..q] has exactly k ele.} =
By lemma 5.1 says E[] =

therefore,
T(n) <= =

Taking expected values

Rely on and T(max(k-1, n-k)) being independent RV. in order to apply C.23

Looking at the expr. max(k-1, n-k)

• if n is even, each term up to appears exactly twic in the sum
• if n is odd, these terms appear twice and appears once
• either way,

Solve this recurrence by substitution,

• Guess that
• Assume for n < some constant
• Also pick s.t. function described by the is bounded from above by

• Choose s.t.

Thus,
assume for , we have

Selection in worst-cace linear time

SELECT works on an array of n > 1 ele.

1. Divide the n ele. into group of 5
   • Get groups
   • groups with exactly 5 ele.
   • if 5 do not divide n, one group with the remaining n mod 5 ele.
2. fin the median of the groups
   • run insertion sort on each group, take time per group ( each group has 5 ele.)
   • pick the median in time
3. find the median of the medians by recursive call to SELECT
   • if is even, find the lower median
4. Using PARTITION takes pivot ele. as input
   • let x be the kth ele.
   • there are k-1 ele. on the lower side
   • n-k ele. on the high side
5. there are 3 possibilities
   • if i=k, just return x
   • if i<k, return ith smallest ele. on the lower side
   • if i>k, return the (i-k)th smallest ele. on the high side

Analyse

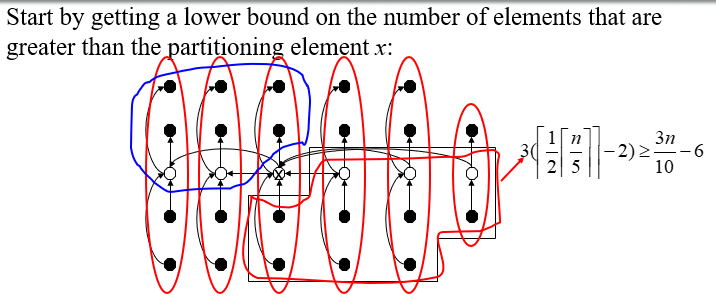
• each group is a col.
• each white circle is a median of a group, as found in step2
• Arrows go from larger ele. to smaller ele., based on what we know after step 4
• ele.in the region on the lower right is greater than x

element

• at least half of the median found in step 2 x
• Look at the groups containing these medians that are x
  • all of them contribute 3 ele. that are x
  • except the group contains x & the group 5 ele.
• forget about these 2 group
  • groups with 3 ele. x
• thus, at least ele. are x

symmetrically, the number of ele. x is
therefore, when call SELECT recursively in step 5, it’s on ele.

Develop, T(n)

• step 1,2 and 4 each take time
  • step 1: making groups of 5 ele. takes time
  • step 2: sorting groups in time each
  • step 4: partitioning the n-ele. array around x takes times
• step 3 takes time
• step 5 takes time , assuming that is monotonically increasing

Assume for small enough n, using n 140
thus, get the recurrence
$$
T(n) \leq
\left{

\right.
$$

solve it by substitution:

• pick a constant s.t. the fun. described by term

• last equation if
  

sinc we assum , we have
thus,
so choosing
gives
in term gives us

end up

SELECT and RANDOMIZED-SELECT
determine information about the relative order of elements
only by comparing elements

• sorting requires time
• sorting algo. runs in linear time, need to make some asssumption
• linear-time selection algo. do not require assumption
• linear-time selection solve problem without sorting, thus not subject to lower bound