Compiler CH4 Grammars and Parsing
Compiler CH4 Grammars and Parsing
Parsing: Syntax Analysis
- decides which part of the incoming token stream should be grouped together.
- the output of parsing is some representation of a parse tree.
- intermediate code generator transforms the parse tree into an intermediate language.
Comparisons between reqular expr. and context-free grammars
A context-free grammar:
𝑒𝑥𝑝→exp〖𝑜𝑝 exp|(𝑒𝑥𝑝)〗 |𝑛𝑢𝑚𝑏𝑒𝑟
𝑜𝑝→+|−|∗A regular expression:
𝑛𝑢𝑚𝑏𝑒𝑟=𝑑𝑖𝑔𝑖𝑡 〖𝑑𝑖𝑔𝑖𝑡〗^∗
𝑑𝑖𝑔𝑖𝑡=0|1|2|3|4|5|6|7|8|9The major difference is that the rules of a context-free grammar are recursive.
Rules from F.A. to CFG
- For each state there is a nonterminal symbol.
- If state 𝐴 has a transition to state 𝐵 on symbol 𝑎, introduce 𝐴→𝑎𝐵.
- If 𝐴 goes to 𝐵 on input 𝜆, introduce 𝐴→𝐵.
- If 𝐴 is an accepting state, introduce 𝐴→𝜆.
- Make the start state of the NFA be the start symbol of the grammar.
Ex.
Why do not we use c.f.g to replac r.e?
r.e. => easy & clear description for token.
r.e. => efficient token recognizer
modularizing the components (The grammar rules use regular expressions as components)
Feature of programming language
contents:
- declarations
- sequential statements
- iterative statements
- conditional statements
Description of programming language
- Syntax Diagrams
- Context Free Grammars (CFG)
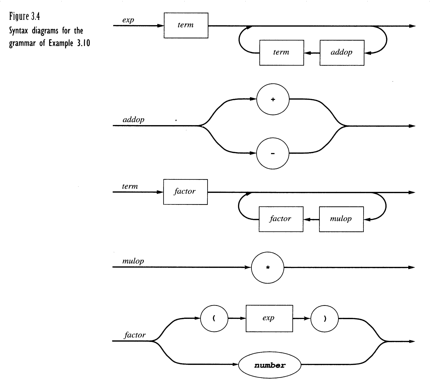
Capabilities of Context-free grammars
- give precise syntactic specification of programming languages
- a parser can be constructed automatically by CFG
- the syntax entity specified in CFG can be used for translating into object code.
- useful for describing nested structures such as balanced parentheses, matching begin-end’s, corresponding if-then-else, etc.
Context-Free Grammars: Concepts and Notation
- A context-free grammar 𝐺=
- A finite terminal vocabulary
- The token set produced by scanner
- A finite set of nonterminal vocabulary
- Intermediate symbols
- A finite terminal vocabulary
- A start symbol 𝑆∈
that starts all derivations - Also called goal symbol
- 𝑃, a finite set of productions (rewriting rules) of the form
- 𝐴→𝜆 is a valid production
Derivation
- One step derivation
- If 𝐴→𝛾, then 𝛼𝐴𝛽⇒𝛼𝛾𝛽
- One or more steps derivation ⟹^+
- Zero or more steps derivation ⟹^∗
If 𝑆⟹
- SF(G) is the set of sentential forms of grammar G (may contain nonterminal vocabulary )
𝐿(𝐺)={
𝐿(𝐺)=SF(G)∩
回溯CFG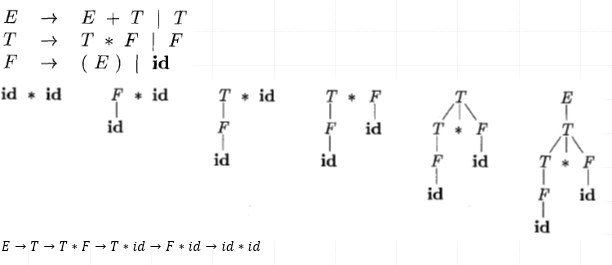
Errors in Context-Free Grammars
unless nonterminal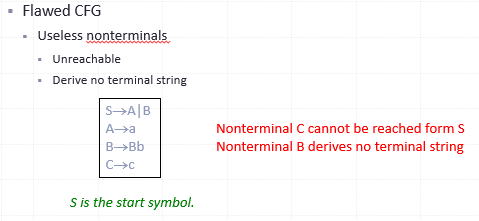
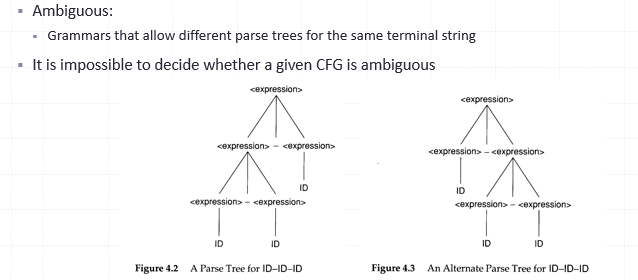
ambiguous
- rewrite CFG
- specifying the intention(使用括號)
Transforming Extened BNF Grammars
Extended BNF≡BNF
- Extended BNF allows
- Square bracket []
- Optional list {}
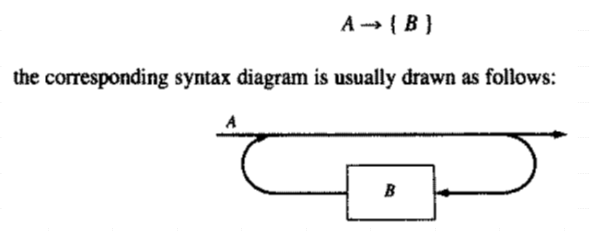
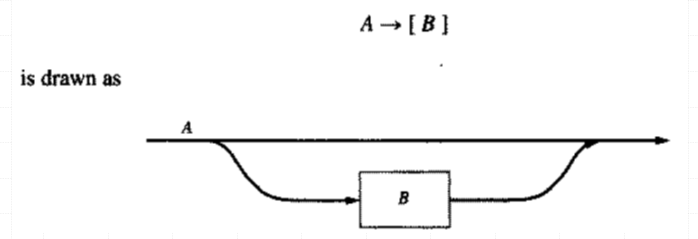
Parsers and Recognizers
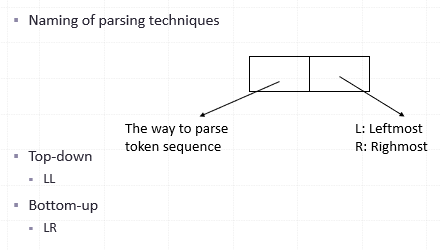
Two general approaches to parsing
- Top-down parser
- Expanding the parse tree (via predictions) in a depth-first manner
- Preorder traversal of the parse tree
- Predictive in nature
- lm
- LL
- Buttom-down parser
- Beginning at its bottom (the leaves of the tree, which are terminal symbols) and determining the productions used to generate the leaves
- Postorder traversal of the parse tree
- rm
- LR
Grammar Analysis Algorithms
Goal of this section
- discuss a number of important analysis algo. for grammars
Cont’d
- data structure of a grammar G

what nonterminals can derive
- A => BCD => BC => B =>
- An iterative marking algo.

ex.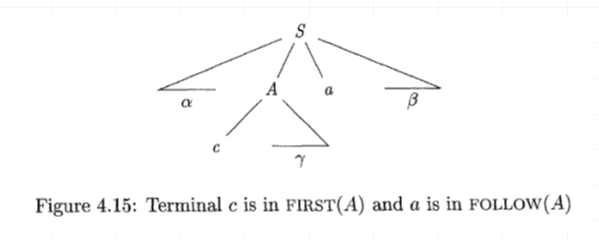
Rule
Follow(A)
- A is any nonterminal
- Follow(A) is the set of terminals that may follow A in some sentential form (跟隨在A後面的終止符號)
- $Follow(A) = {a \in V_t | S=> ^* …Aa…} \cup {if, S=> ^+aA , then , \
Compiler CH4 Grammars and Parsing
https://z-hwa.github.io/webHome/[object Object]/Compiler/Compiler-CH4-Grammars-and-Parsing/