Computer Organization CH3 Arithmetic for Computeres

3.1 Introduction

Chapter Goals

To understand

• representation of real numbers
• arithmetic algo.
• hardware that follows these algo.
• the implications(影響) of all this for instruction sets

Show how this knowledge to make arithmetic-intensive programs go much faster

3.2 Addition and Substraction

Integer Addition

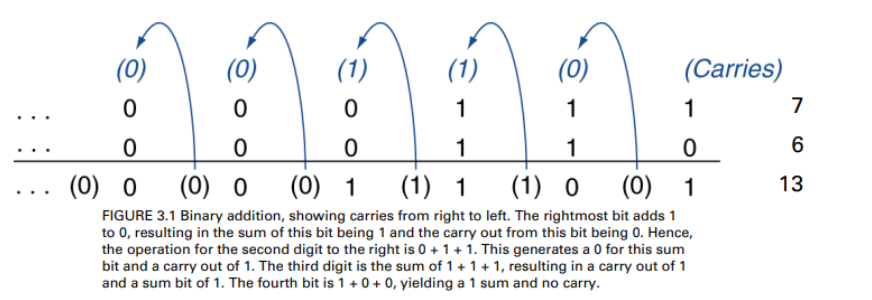
• Ex. 7+6
• Overflow cannot occur
  • when adding operands with diff. signs, since the sum must be no larger than one of the operands (if the operands fit in 32 bits)
• Overflow occur if the result is out of range
  • Adding +num, -num operands -> no overflow
  • Adding two +num operands
    • overflow if result sign is 1
  • … two -num operands
    • overflow if result sign is 0
  • 就是同號數字相加，結果卻變號了

Integer Substraction

Concept: negate the second operand, than add

• Ex. c-b = c+(-b)

Example: 7+(-6)

• -6 users two’s compliment repr.
• 

Overflow cannot occur

• when the signs of the operands are the same

Overflow occur

• two +num or -num operands -> no overflow
• +num minus -num operand
  • overflow if result sign is 1 (<0)
  • 被減數是正的，減數是負的，結果卻是負數
  • Ex. 8-(-2)
• -num minus +num operand
  • overflow if result sign is 0 (>=0)

The above shows how to detect overflow for
two’s complement numbers in a computer

About unsigned integer

• compile using a branch instruction
• Addition overflow: the sum is less than either of the addends
• Substraction overflow: the difference is greater than the minuend

what will happen when overflow occur?
-> saturating operations(飽和操作) in multimedia apps

• E.g., clipping in audio(音訊中的削波), saturation in video(視訊中的飽和度)
• on overflow, result is largest repr. value
• compare w/2’s-complement modulo arithmetic

Basic Arithmetic Logic Unit(ALU)

ALU is hardware

• performs addition, substraction
• logical operations
  • AND/OR

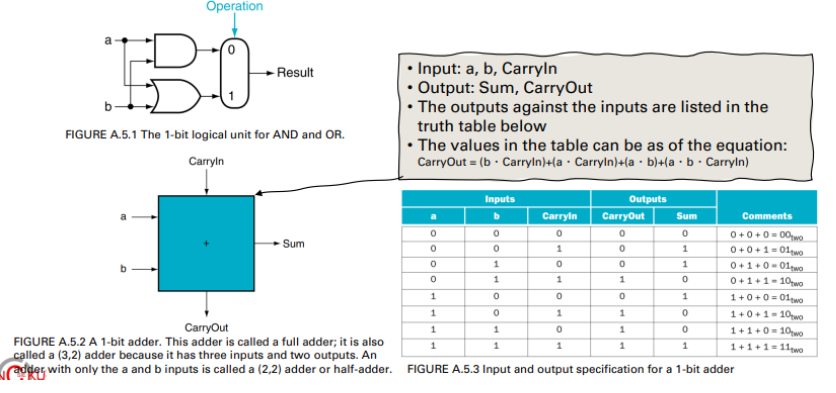
More on ALUs

• A 1-bit ALU
  

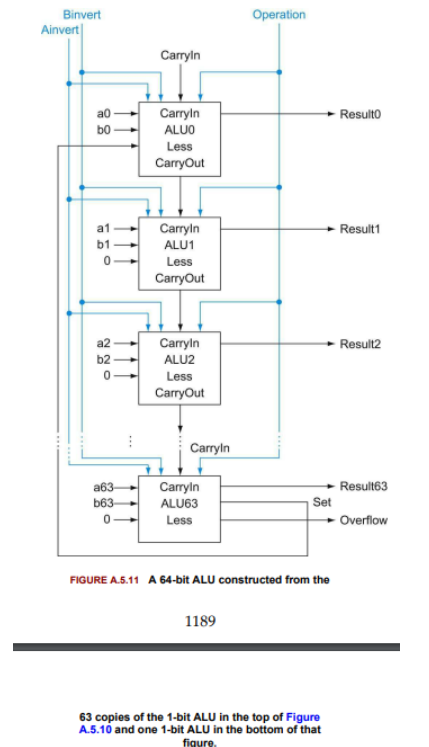
• 32-bit ALUs

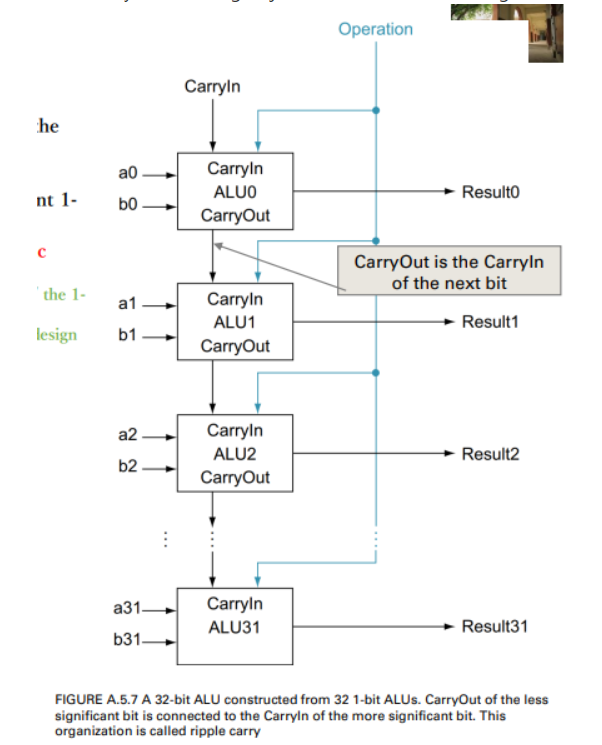
  • created by connecting adjacent 1-bit ALUs as in Fig. A.5.7
    

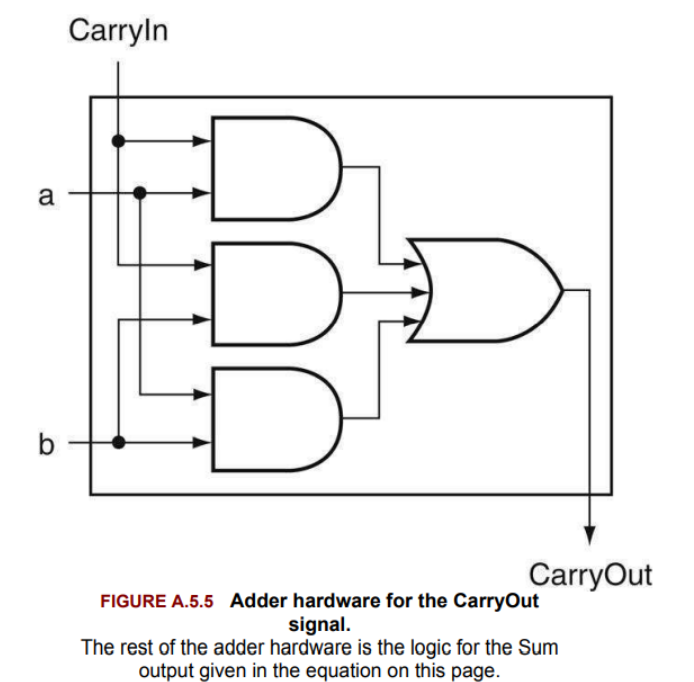
• Adder hardware for the CarryOut signal
  

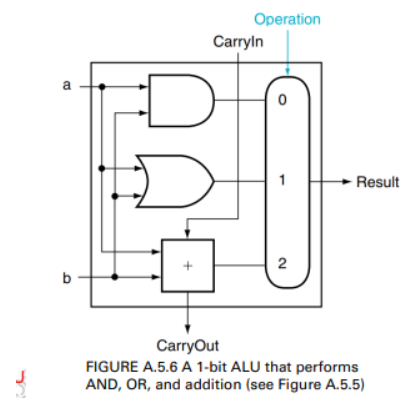
• A 1-bit ALU that performs AND, OR, and addition on a and b or and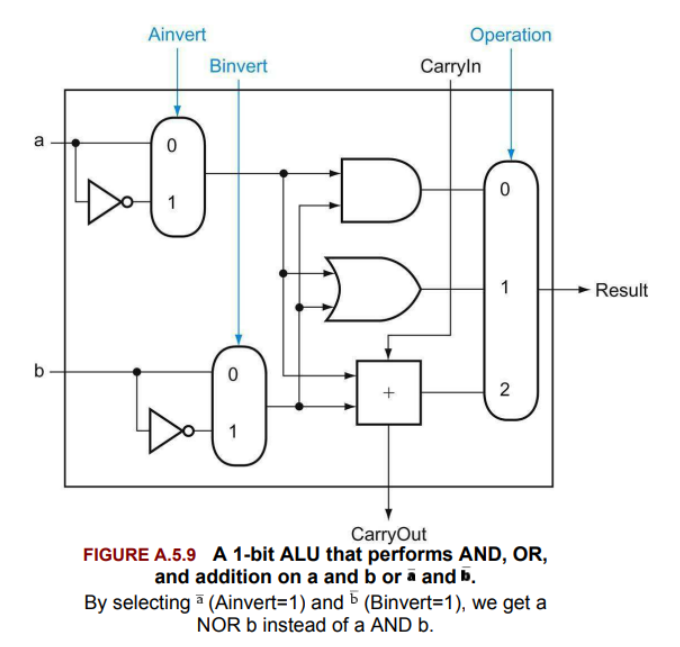
  

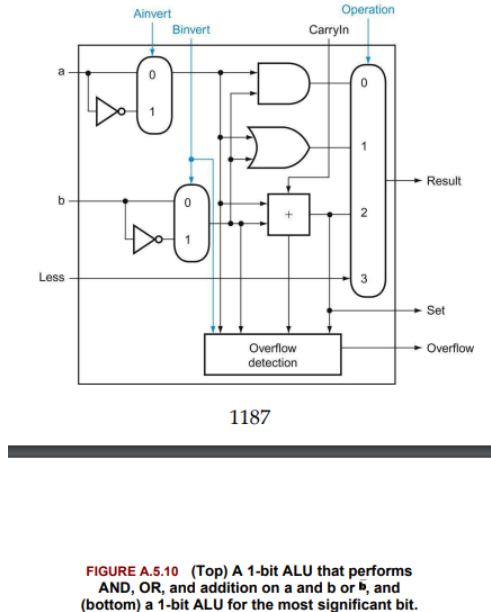
• handle overflow
  

• A 64-bit ALU constructed from the 63 copies of the 1-bit ALU in the top of Figure A.5.10 and one 1-bit ALU in the bottom of that figure
  

3.3 Multiplication

Multiplication

Procedure for binary multiplication

1. take the digits of multiplier one at a time from right to left
2. multiply the multiplicand
3. shift the intermediate product one digit to the left of the earlier intermediate products
   

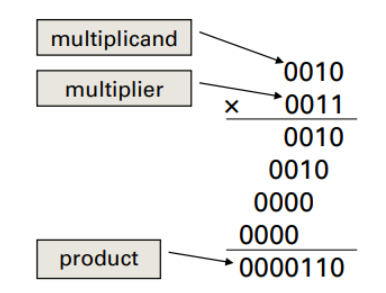
The length of product

• larger than the nuber in either multiplicand or the multiplier
  • overflow may occur

32-bit data

Three step in Fig.3.4

• the control flow of binary multi. in the previous
  

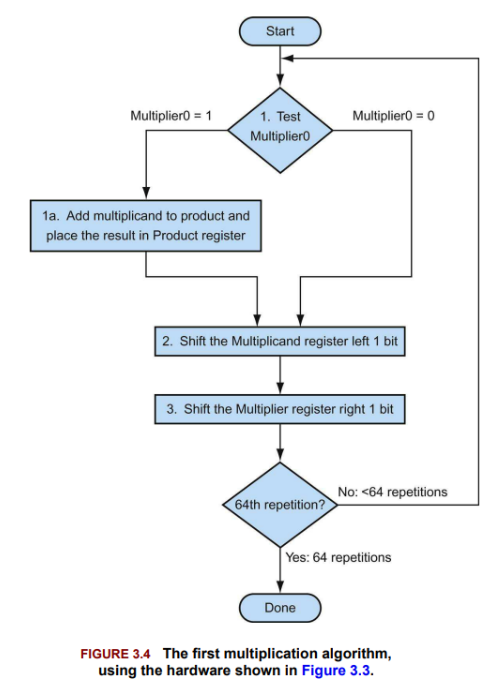
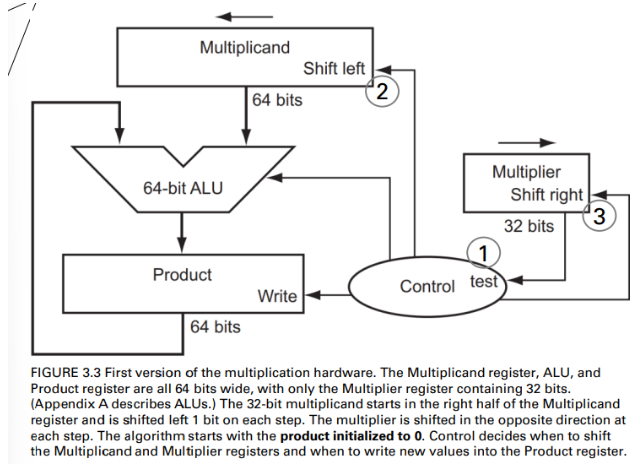
• First version of multi. hardware
  

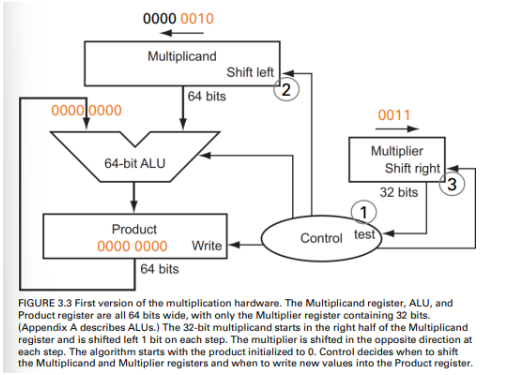
Example

• Init
  • 4-bit multiplie
  • 8-bit ALU
  • 8-bit multiplicand
  • 8-bit product

• step iter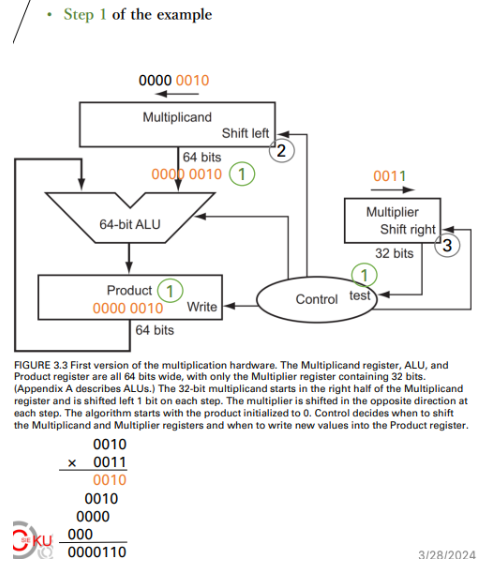
  

• step and iter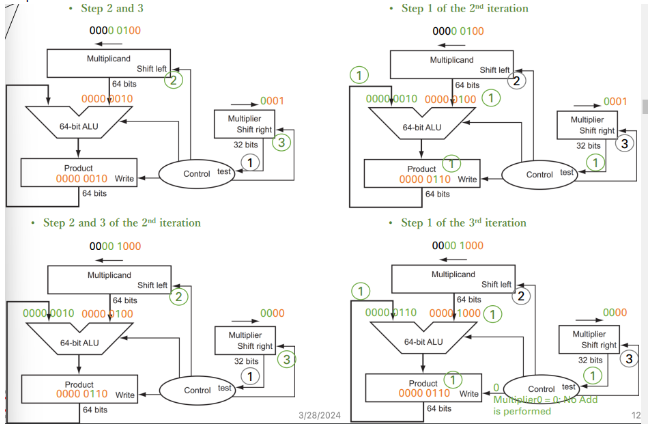
  

• step iter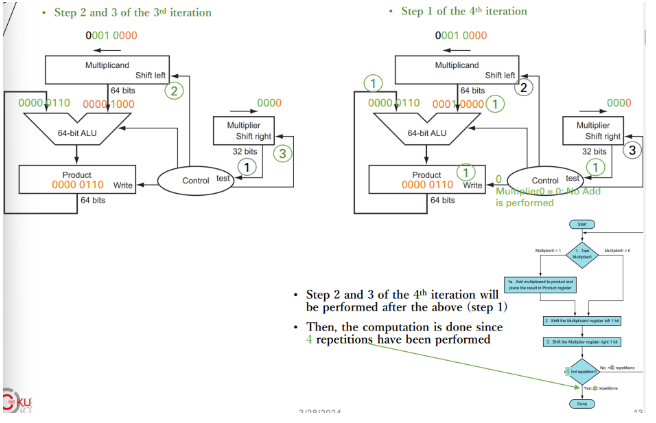
  

RISC-V inst.

Four multiply instructions to produce 64-bit products

• mul: multiply
  • Gives the integer 32-bit product (from the lower 32-bit of the 64-bit product)
• mulh: multiply high
  • Gives the upper 32 bits of the 64-bit product (if the both operands are signed)
• mulhu: multiply high unsigned
  • Gives the upper 32 bits of the 64-bit product (if the both operands are unsigned)
• mulhsu: multiply high signed/unsigned
  • Gives the upper 32 bits of the 64-bit product (if one operand is signed and the other unsigned)
• Use mulh result to check for 64-bit overflow Check p. 198-199 of textbook for details

Example: code sequence to get the product of unsigned
multiplication

mulh rdh, rs1, rs2
mul rdl, rs1, rs2

• The multiplicand and multiplier are kept in rs1 and rs2, respectively
• The high/low 32 bits data are in rdh and rdl, respectively

3.4 Division

Division

Exam if divisor is equal to 0

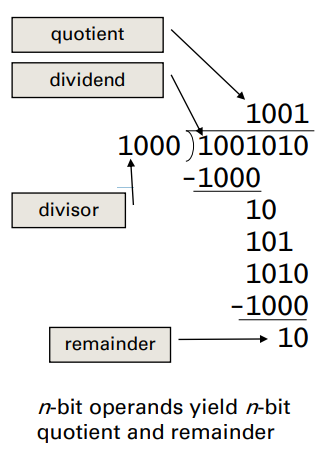
Long division approach

• If bit len(divisor) ≤ len(dividend)
  • 1 bit in quotient, subtract
• Otherwise
  • 0 bit in quotient, bring down next dividend bit
• Restoring division (for HW impl.)
  • Do the subtract, and if remainder goes < 0, add divisor back
• Signed division
  • Divide using absolute values
  • Adjust sign of quotient and remainder as required

RISC-V division inst.

Four instructions for signed integers and unsigned integers

• div (divide), rem (remainder): for signed division and reminder
• divu (divide unsigned), remu (remainder unsigned): for unsigned division and reminder

3.5 Floating Point

Floating Point

Representation for non-integral numbers

• Numbers with fractions, called reals in mathematics
• Including very small and very large numbers
• E.g., 3.14159… (pi), 2.71828… (e)
• Computer arithmetic that supports such numbers is called floating point

Scientific notation is an alternative notation for numbers

• The notation has a single digit to the left of the decimal point

In binary (base 2), the form is as below with a single nonzero digit to the left of the binary point

• ×
• ×

Data types float and double in C

Floating-point representation

A floating-point representation must find a
compromise between the size of the fraction and the size of the exponent, given a fixed bit-width register

• Fraction (or mantissa) is the value, generally between 0 and 1, placed in the fraction field
• Exponent is the value placed in the exponent field in the numerical representation system of floating-point arithmetic

A floating-point numbers is often of the form:

IEEE 754 Floating-point standard

S: sign bit

• 0 => non-negative, 1 => negative

Fraction

• Always has a leading pre-binary-point 1 bit, so no need to represent it explicitly (but it is a hidden bit in IEEE 754)
  • It is 23 bits in single precision and 52 bits in double precision
• Normalize significand: 1.0 ≤ |significand| < 2.0; e.g.,
• Significand = 1 + Fraction
  • It is actually 24 bits in single precision and 53 bits long in double precision

Exponent

• An stored exponent = actual Exponent + Bias
• Ensures Exponent is unsigned
• Bias for single precision: 127, for double precision: 1023
• E.g., an actual exponent of −1 is represented by the bit pattern of the value −1 (Exponent) + 127ten, or 126ten = 0111 1110two

If we number the bits of the fraction from left to right s1, s2, s3, …, then the value can be computed via the formula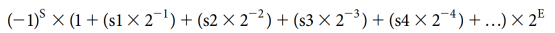

Range of single precision numbers

Exponents 00000000 and 11111111 are reserved

Smallest value

• Exponent: 00000001
• actual exponent = 1 – 127 = –126
• Fraction: 000…00 => significand = 1.0
• I.e., × → ≈

Largest value

• exponent: 11111110
• actual exponent = 254 – 127 = +127
• Fraction: 111…11 => significand ≈ 2.0
• I.e., × → ≈

Range of double precision numbers

Exponents 0000…00 and 1111…11 are reserved

Smallest value

• Exponent: …00000000001
• actual exponent = 1 – 1023 = –1022
• Fraction: 000…00  significand = 1.0
• ≈

Largest value

• Exponent: …11111111110
• actual exponent = 2046 – 1023 = +1023
• Fraction: 111…11  significand ≈ 2.0
• ≈

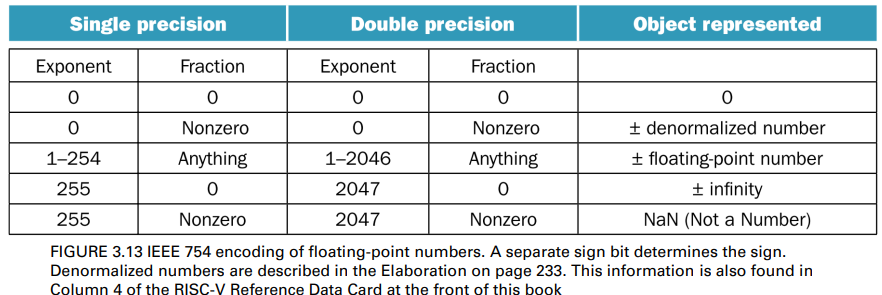
Encoding of IEEE 754 numbers

Different bit patterns serve for different purposes

• E.g., to represent the value of 0 (Use IEEE 754 format to represent a Zero)
• E.g., to indicate the result of invalid operations via NaN, such as 0/0 or subtracting infinity　from infinity

The reserved data values are used for indicating the special values

A new, revised standard IEEE 754-2008 is released in 2008

• It includes nearly all the IEEE 754-1985 and adds a 16-bit format (“half precision”) and a 128-bit format (“quadruple precision”)
• Half precision has a 1-bit sign, 5-bit exponent (with a bias of 15), and a 10-bit fraction
• Quadruple precision has a 1-bit sign, a 15-bit exponent (with a bias of 262,143), and a 112-bit fraction

Example

The IEEE 754 binary representation of in single precision

• S = 1
• Fraction =
• Exponent = -1 (actual exponent) + Bias = 126
  • single: -1 + 127 = 126 =

The bit form of -0.75 in 32-bit register: 1011111101000…00

Please check the bit form of -0.75 in double precision by yourself

• Bias = 1023

Special Number(Infinities, NaNs, etc.)

Exponent = 111…1, and Fraction = 000…0

• ± ∞ (Infinity)
• This encoding scheme indicates that the number can be used in subsequent calculations, avoiding need for overflow check
• E.g., F+(+∞) = + ∞, F/∞=0

Exponent = 111…1, and Fraction ≠ 000…0 (nonzero)

• It indicates Not-a-Number (NaN)
• NaN is illegal or undefined result
  • E.g., 0.0 / 0.0
• Can be used in subsequent calculations

Exponent = 000…0, and Fraction ≠ 000…0 (nonzero)

• ± denormalized numbers
• Please refer to the Elaboration section in page 233 for special numbers

標準的浮點數就是之前我們所定義的浮點數的表示法
大家應該有印象 在fraction或者是significand的前面
也就是小數點前面 我們有一個hidden的leading 1
前面有一個1做為開頭 而在denormalized的number裡面 我們讓這個1不見
也就是說我們讓小數點的開頭變成是0 而後面接上significand
透過這樣子的設計 因為少了這個leading的1 實際上我們就可以表達出更小的數字了

解釋

為了要讓fraction不為0的情況 也可以拿來表達一些浮點數的特殊情況的話
我們採取的做法就是讓fraction當它不等於0的時候 而exponent等於0的時候
我們讓前面的這個leading變成0
既然是0開頭的 實際上後面這一串它是不等於0的
可是它能夠表達的數字就會比前面我們剛才所談到最小的 合法的浮點數它表達的數字範圍的最小值來的更小

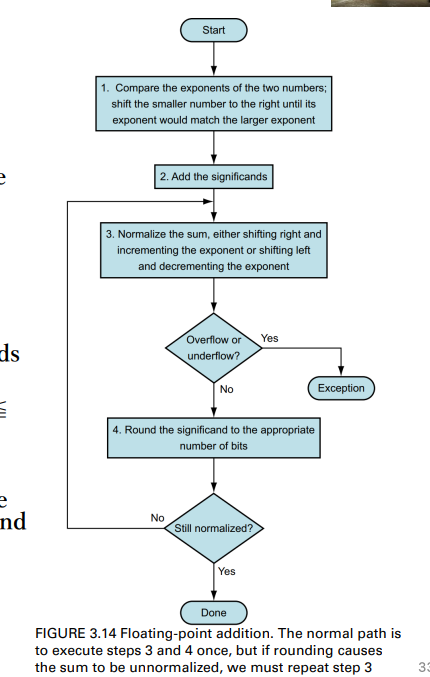
Floating-point Addition Procedure

1. Match the exponents of the two numbers

   • By adjusting the significand of the number with the smaller exponent to be the same with the larger exponent

2. Add the two significands

3. Normalize the result and check for overflow or underflow

   • The test for overflow and underflow depends on the precision of the operands
   • Refer to Fig. 3.13 for bit patterns
   • In single precision, -126 ≦ Exponent ≦ 127

4. Round the number(取整)

   • Round up: truncates the digit if 0 ≦ the digit to the right of desired digit ≦ 4, and
   • Round down: add 1 to the digit if 5 ≦ the number to the right ≦ 9
   • Perform Step 3 after rounding, if necessary, since the data is no longer normalized

Addition Ex.

Now consider a 4-digit binary example (p. 216 in textbook)

• To obtain the sum for the following two numbers
• :
• :

1. Match exponents

• Shift number with smaller exponent (i.e., )

2. Add significands

3. Normalize result & check for over/underflow

• with no over/underflow

4. Round (into 4 bits) and renormalize if necessary

• (no change) (= 0.0625ten)

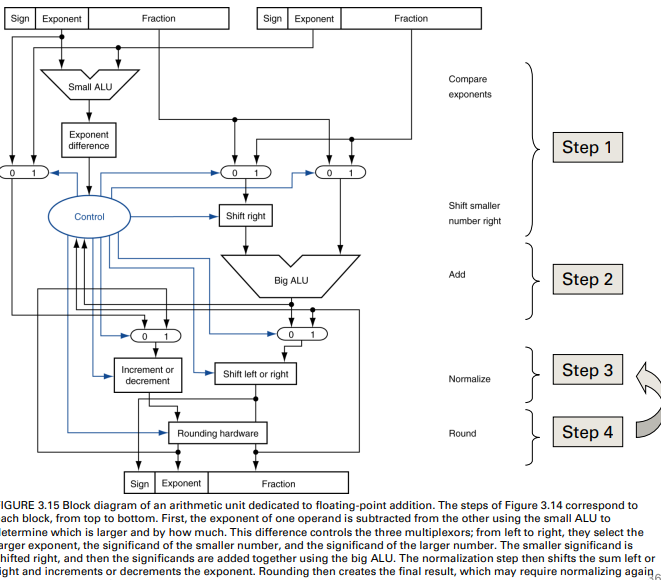
Floating-point adder

Much more complex than integer adder

Doing it in one clock cycle would take too long

• Much longer than integer operations
• Slower clock would penalize all instructions

FP adder usually takes several cycles

• Can be pipelined(可流水線化)

Floating-Point Multiplication Procedure

1. Calculate the exponent of the product
   • by adding the exponents directly if the operands together
   • *Or, you can calculate with the biased exponents
2. Multiplication of the significands
   • Be aware of the placement of the binary point of the product
3. Normalize the product
   • Also check for overflow and underflow
4. Round the number
   • to fit the desired digits length (e.g., 4 digits)
5. Use proper sign of the product
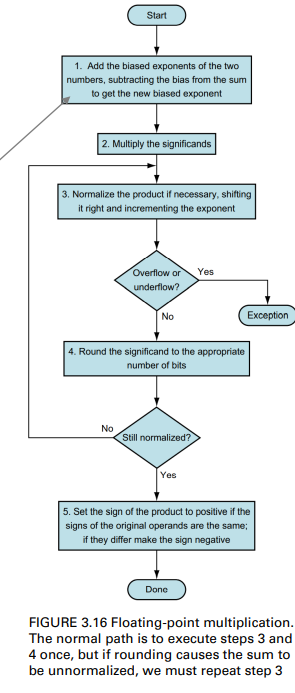
   • If the original operands are both the same sign, the sign of the product is positive; otherwise, it’s negative

Ex.

Floating-point(FP) Arithmetic Hardware

FP multiplier is of similar complexity to FP adder

• But uses a multiplier for significands instead of an adder

FP arithmetic hardware usually does

• Addition, subtraction, multiplication, division, reciprocal, square-root
• FP <-> integer conversion

Operations usually takes several cycles

• Can be pipelined

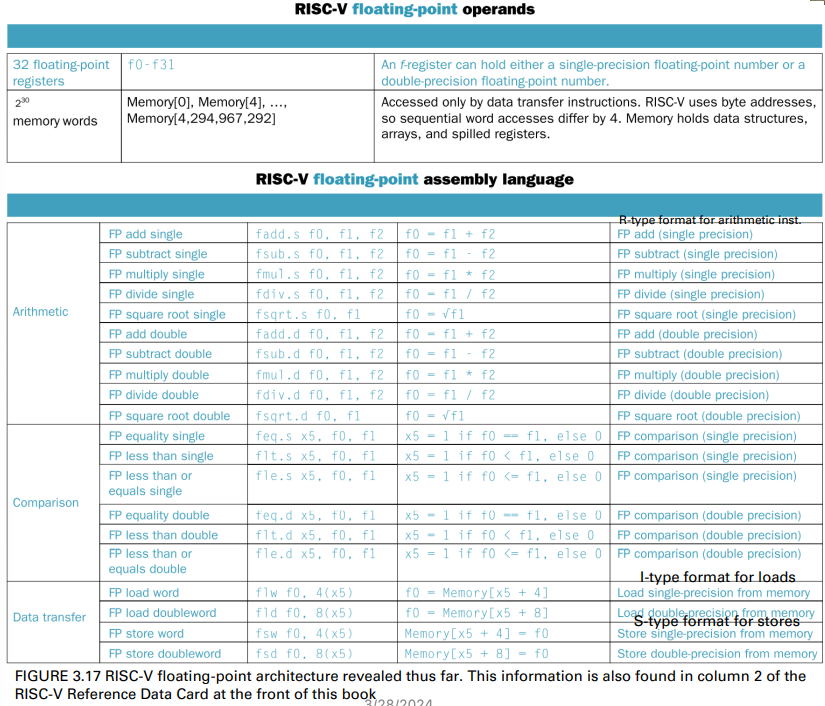
The RISC-V designers decided to add separate
floating-point registers (32 registers)(新增的浮點暫存器)

Inst.

A separate set of FP registers: f0, …, f31

• A single precision register is just the lower half of a doubleprecision register
• I.e., single-precision values stored in the lower 32 bits
• NOTE: f0 is not hard-wired to the constant 0

FP instructions operate only on FP registers

• Programs generally don’t do integer ops on FP data, or vice versa
• More registers with minimal code-size impact
• Include FP load/store and arithmetic instructions

FP load and store instructions

• Single-precision load/store: flw, fsw
• Double-precision load/store: fld, fsd

Inst. with IEEE 754 Format

Single-precision arithmetic

• fadd.s, fsub.s, fmul.s, fdiv.s, fsqrt.s
  • e.g., fadd.s f2, f4, f6

Double-precision arithmetic

• fadd.d, fsub.d, fmul.d, fdiv.d, fsqrt.d
  • e.g., fadd.d f2, f4, f6

Single- and double-precision comparison

• feq.s, flt.s, fle.s
• feq.d, flt.d, fle.d
• Result is 0 or 1 in integer destination register
  • Use beq, bne to branch on comparison result

Branch on FP condition code true or false

• B.cond

Accurate Arithmetic

IEEE Std 754 specifies additional rounding control

• Extra bits (in circuitry) of precision (guard, round, sticky)
• Choice of four rounding modes
  1. always round up (toward +∞)
  2. always round down (toward −∞)
  3. truncate
  4. round to nearest even
• Allows programmer to fine-tune numerical behavior of a computation

Not all FP units implement all options

• Most programming languages and FP libraries just use defaults
• Java only supports the fourth mode above

Trade-off(權衡) between hardware complexity,
performance, and market requirements

from https://blog.csdn.net/qianniuwei321/article/details/113499393

Ex.

• convert a temperature in F. to C.

Accurate Arithmetic

Example of the effect of guard and round

• + (assume the result should be three significant decimal digits)
• With guard/round
  • + = => (round up)
• Without guard/round
  • + =
• is off by 1 (1 ulp) in the last digit from

Measure accuracy with “units in the last place” (ulp)

• The number of bits in error in the least significant bits of the significand between the actual number and the number that can be represented
• Please refer to p. 230 in textbook (IEEE 754 guarantees ½ ulp)

The Big picture bit patterns vs. inst.

Bit patterns have no inherent meaning

• They may represent signed integers, unsigned integers, floating-point numbers, instructions, character strings, and so on

What is represented depends on the instruction that
operates on the bits in the word

The major difference between
computer numbers and numbers in the
real world is that computer numbers
have limited size and hence limited
precision

Programmers must remember these
limits and write programs accordingly

3.6 subword parallelism

subword parallelism

把128bit寬的register分割成兩個64bit space

• those 2 part of space could be used to compute two data at the same time

SIMD concept

• single instruction multiple data
• 運算的指令是一樣的，但資料是不同的

可能存在資料轉移的成本

fallacy right shift and division

only under unsigned bit

• right shift the same as division

pitfall

• floating-point addition is not associative

sequence vs. parallel

• in sequence, order is fixed
  • result also
• in parallel, order is not fixed
  • decide by CPU
  • result might diff.
  • caused problem in floating-point
    • which is not associative

there are always 誤差 in computer