Chapter 13 Probabilistic Reasoning
Chapter 13 Probabilistic Reasoning
Representing Knowledge
DAG (有向無環圖)

- 獨立或條件獨立 能夠有效減少需要被定義的機率數量
拓樸的意義是 每個箭頭代表著 父親對孩子有直接的影響

牙齒的案例:


新問題 竊盜警報器:

- DAG
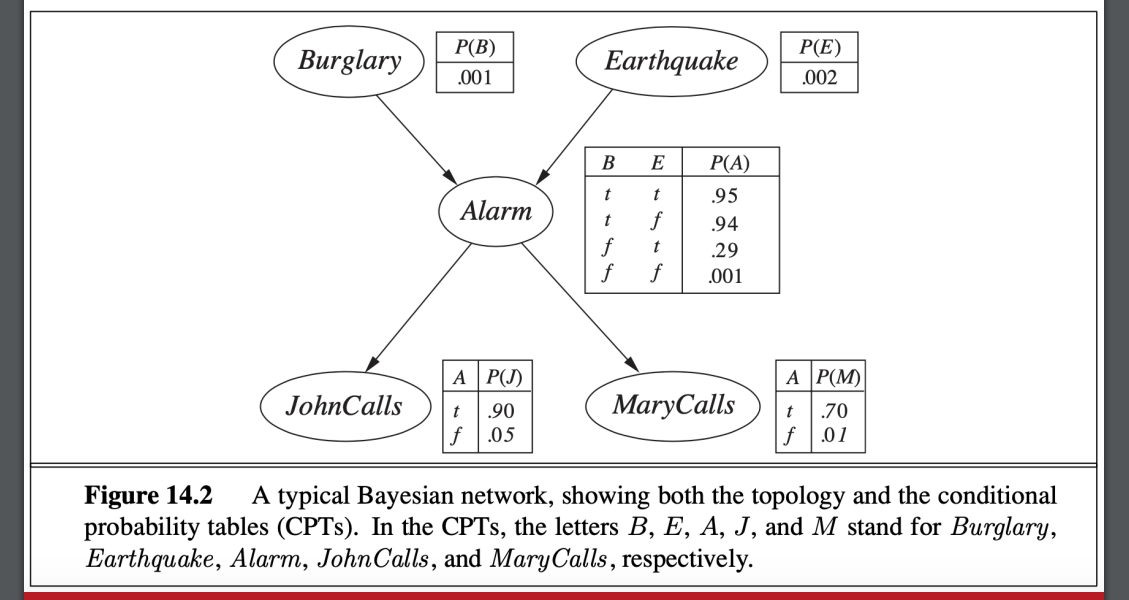
- 表示鄰居的電話 僅直接受警報器影響

- 上上圖中 每個節點旁的表 稱之為 CPT

- 至於鄰居受到的其他影響則被認為是存在於 警報器到兩鄰居之間的不確定性
- DAG
藉此我們能讓小agent 去感受整個世界:

The Semantics of Bayesian Networks
- Bayesian network有兩種解釋

- 當作joint probability distrobution 比較容易建構
- 當作條件獨立敘述的encoding 比較容易設計推理過程
Representing the full joint distribution
一個例子

建構Bayesian network 的方法


- 重複將機率拆解為條件機率

- 實際的步驟
- 重複將機率拆解為條件機率
特性

- 因為每個節點的父親 來自於更早的節點 不可能出現循環
- 沒有 redundant probability value 使用者不可能違反機率的原則

- 某些領域中 每個變數受其他變數的直接影響 => DAG 是fully connected
- 有些領域 變數之間存在微弱的相依性 => 可以考慮不要連線 犧牲一點精確性 減少複雜度

- 例子
好的節點順序很重要

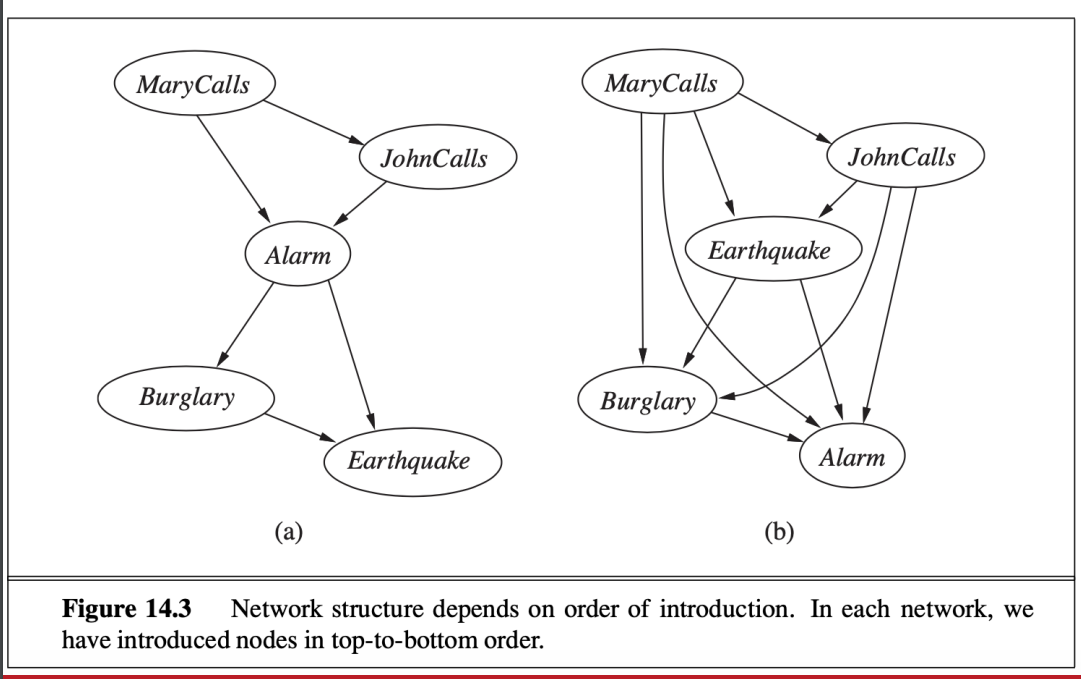
- 否則 圖的複雜度會提高

- 構圖解釋
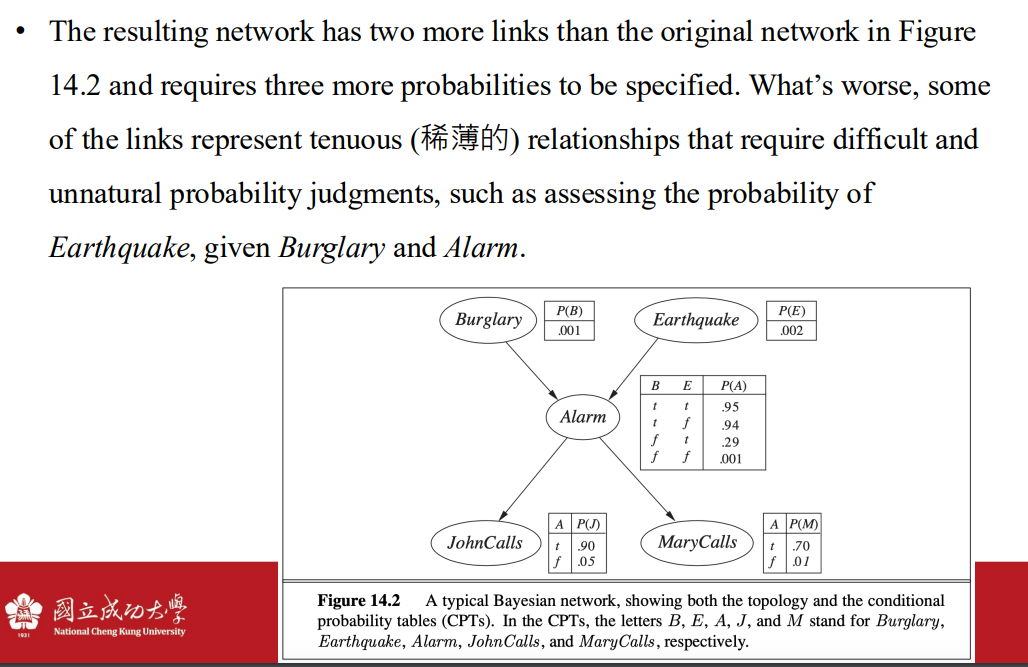
- 這張圖裡面的連接不自然 而且更加複雜

- 而且我們需要額外的連接來表達最終所希望的 診斷到原因的模型 也就是14.3(b)

- 否則 圖的複雜度會提高
Conditional independence relations in Bayesian networks
- 有條件獨立

- Markov blanket
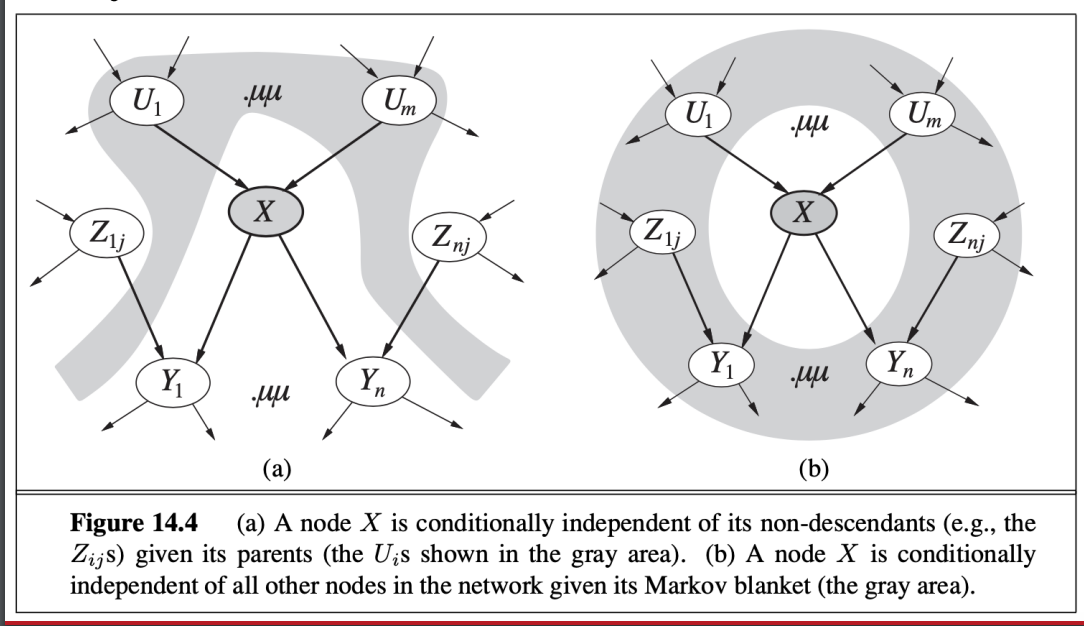
- 灰色區塊
- Markov blanket
Bayesian nets with continuous variables
離散化


- 參數法: 常態分布
- 非參數法: 使用instance 每個instance包含父變數和子變數特定的值
Hybrid bayesian network

- 包含離散以及連續變數
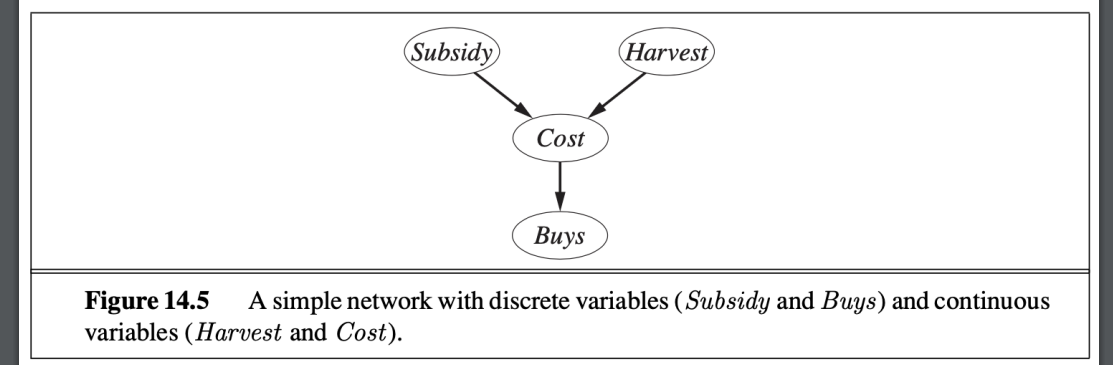
- DAG
- 包含離散以及連續變數
線性高斯分布

- 孩子符合高斯分布: 平均值隨父親線性變化 標準差固定

- 形式
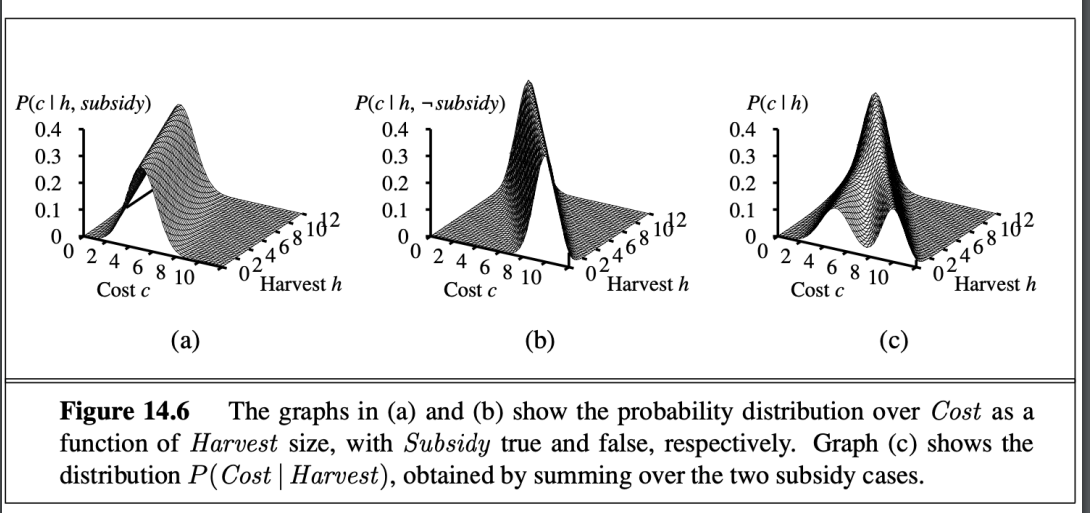
- 圖像化

- 孩子符合高斯分布: 平均值隨父親線性變化 標準差固定
關於購買與否的閾值

- 透過soft threshold function

- 實際的定義
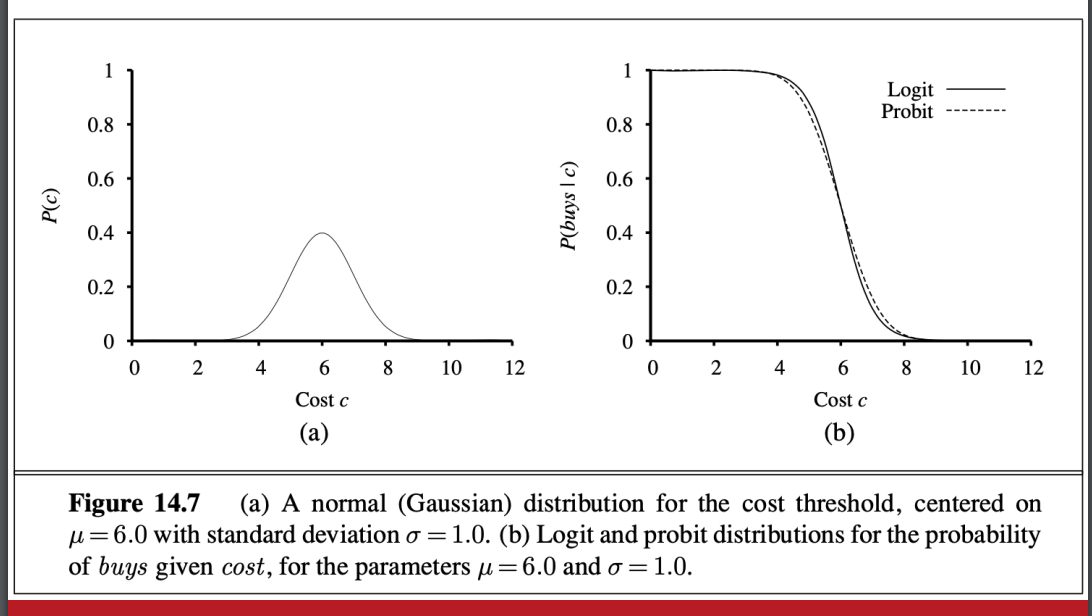
- 圖像化 probit distribution
- 透過soft threshold function
logit distribution

- 更容易數學化 應用在神經網路
Exact Inference in Bayesian Networks
- 實際的推論 找posterior probability distribution


- 例子
Inference by enumeration
推論

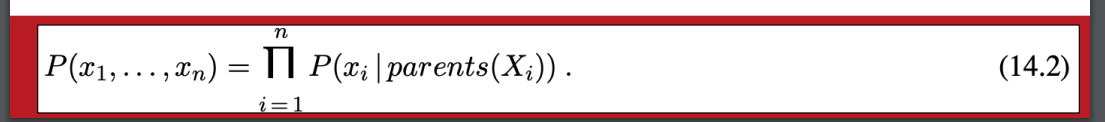
- base on

- 進一步改進形式

- 觀察 簡化
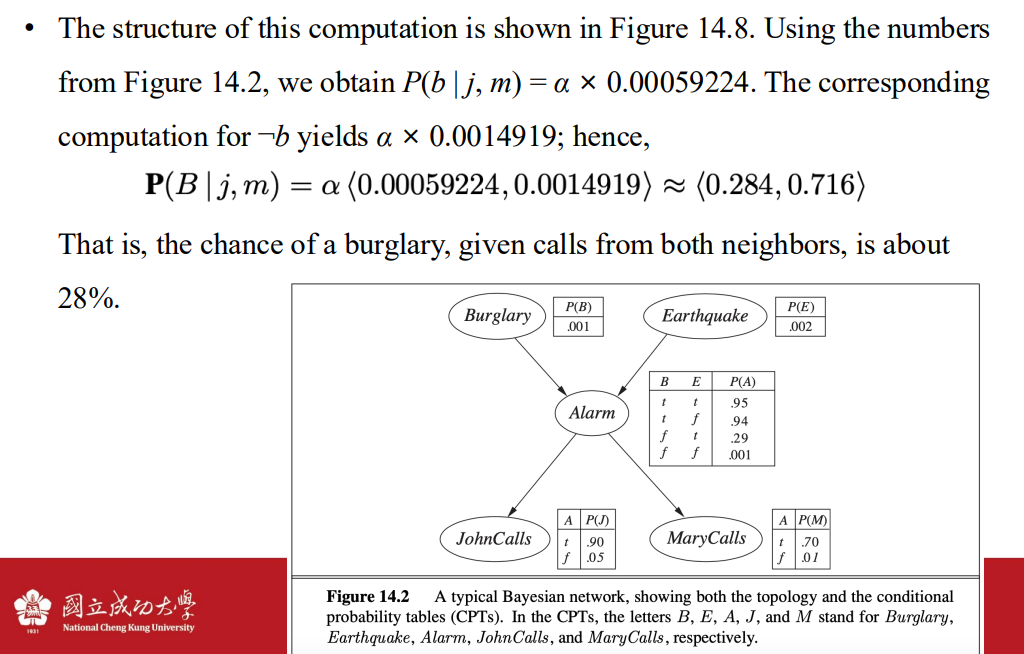
- 計算結果
- base on
計算的架構圖
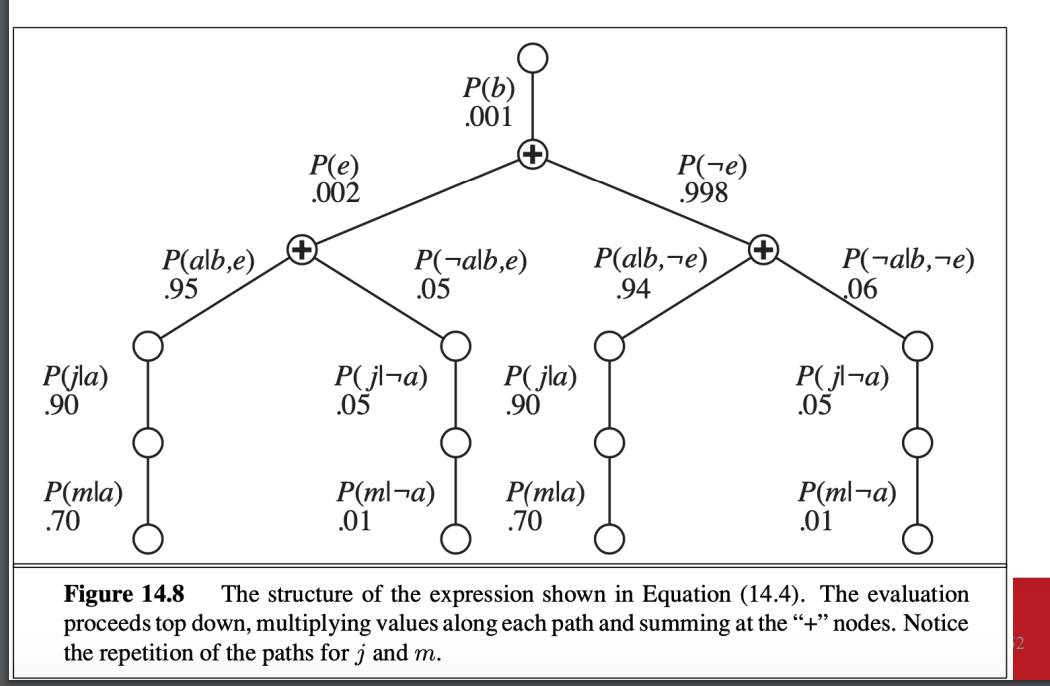
- 由上而下
seudo code

The complexity of exact inference
poly tree
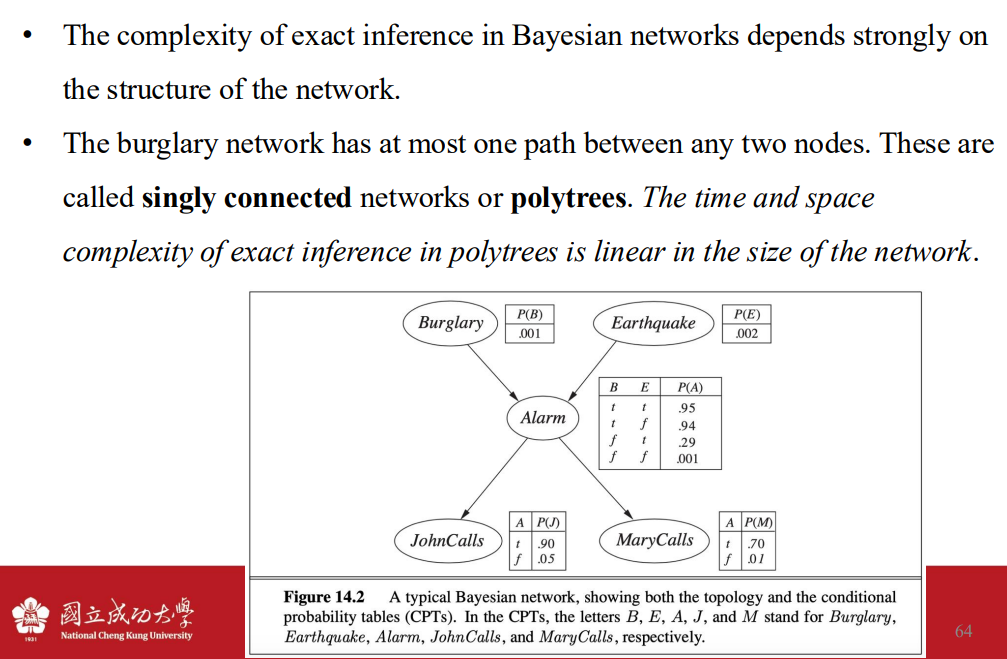
- 推理的complexity 是根據網路的尺寸線性增加
- simply connected: 任意兩點之間只有一條路徑
multiply connected

- hard NP problem
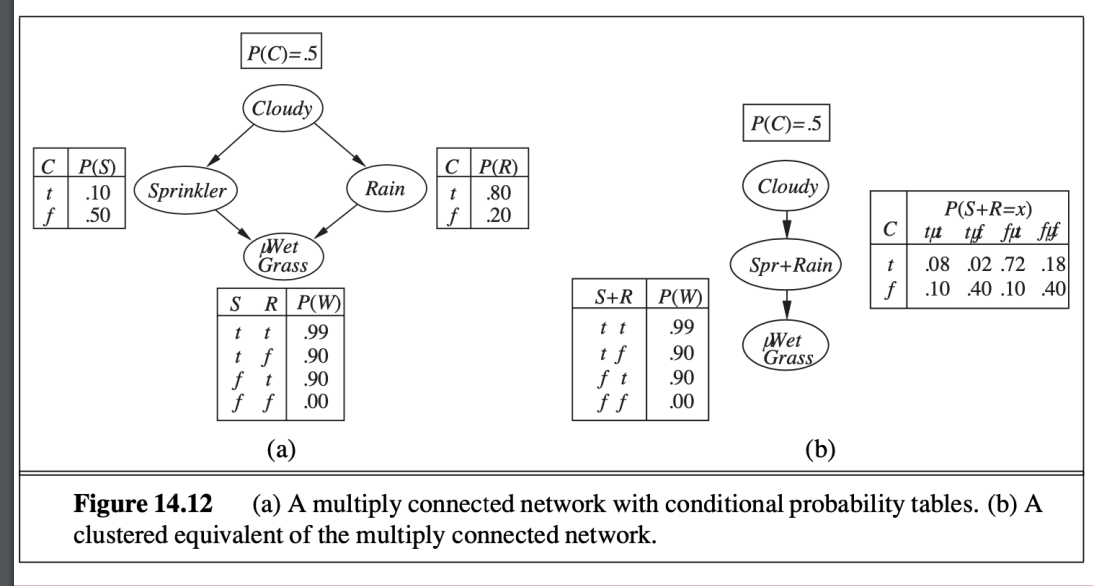
- hard NP problem
Approximate Inference in Bayesian Nets
- Monte Carlo algorithm

- 兩種算法 directr sampling, Markov chain sampling
Direct sampling methods
生成sample


- pseudo code

- 例子

- 該生成sample的機率 可以化成條件機率 根據parent

- 因為算法是從Bayesian network 產生的 所以sample的機率是正確的
- pseudo code
考慮樣本數量


- 藉由直接取樣 我們能簡單估計機率
Rejection sampling

- 取樣後 扣除不符合e的事件 可以估計條件機率

- 正確的原因 以及例子

- 樣本數越多 越接近正確 但問題在於reject 容易拒絕太多樣本了

- 原因可以參考現實世界的情況 => 出現特定證據的情況本來就少
- 取樣後 扣除不符合e的事件 可以估計條件機率
Inference by Markov chain simulation
Marko chain monte carlo

- 部分改變上一個樣本
- Gibbs sampling
Gibbs sampling

- 改變Markov blanket上的隨機變數 固定evidence
- Markov blanket: node’s parent, node’s child, parent of node’s child

- Markov blanket: node’s parent, node’s child, parent of node’s child
- 例子

- 算法解釋

- Pseudo code
- 改變Markov blanket上的隨機變數 固定evidence
Chapter 13 Probabilistic Reasoning
https://z-hwa.github.io/webHome/[object Object]/Introduction to Artificial Intelligence/Chapter-13-Probabilistic-Reasoning/