Chapter 14 Probabilistic Reasoning over Time

Time and Uncertainty

• 靜態假設

  

• 動態情況

  

  • 血糖指數會動態改變

States and observations

• time slice 以及符號定義

  
  

  • 下雨天的例子

• 集合符號的定義

  

  • 本單元假設time slice 是固定的長度 可以用整數表示

Transition and sensor models

• Markov assumption

  

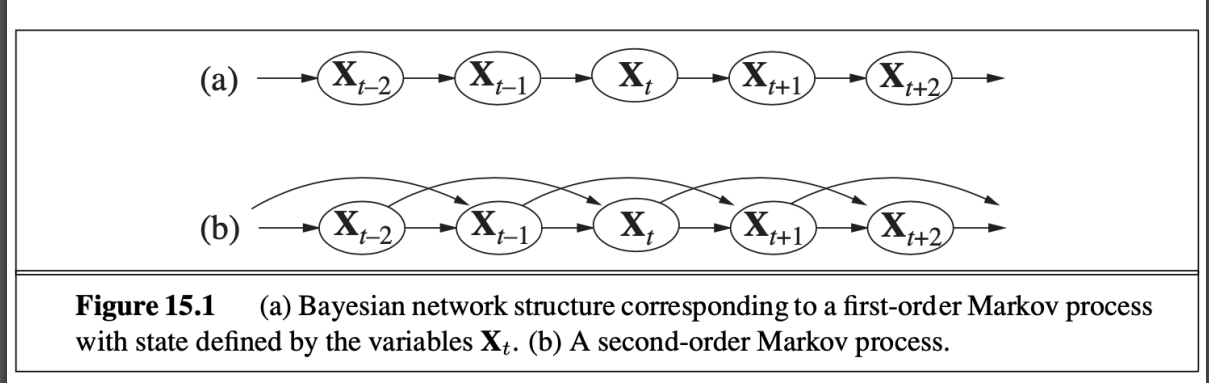
  • 假設當前狀態只與 前k個有限數量的狀態有關

• first oreder, second order Markov assumption => transition model

  

  • 相當於條件機率

    

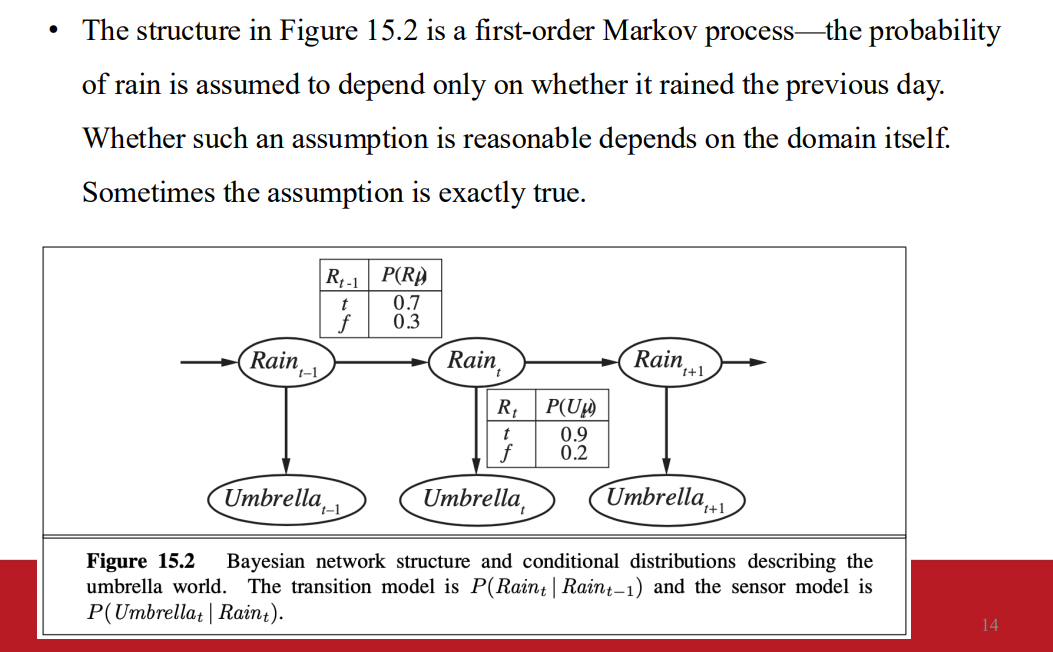
• 雖然是動態世界 但世界狀態改變的法則是固定的

  

  • 機率是固定的 只是時間會變化

• sensor model

  
  

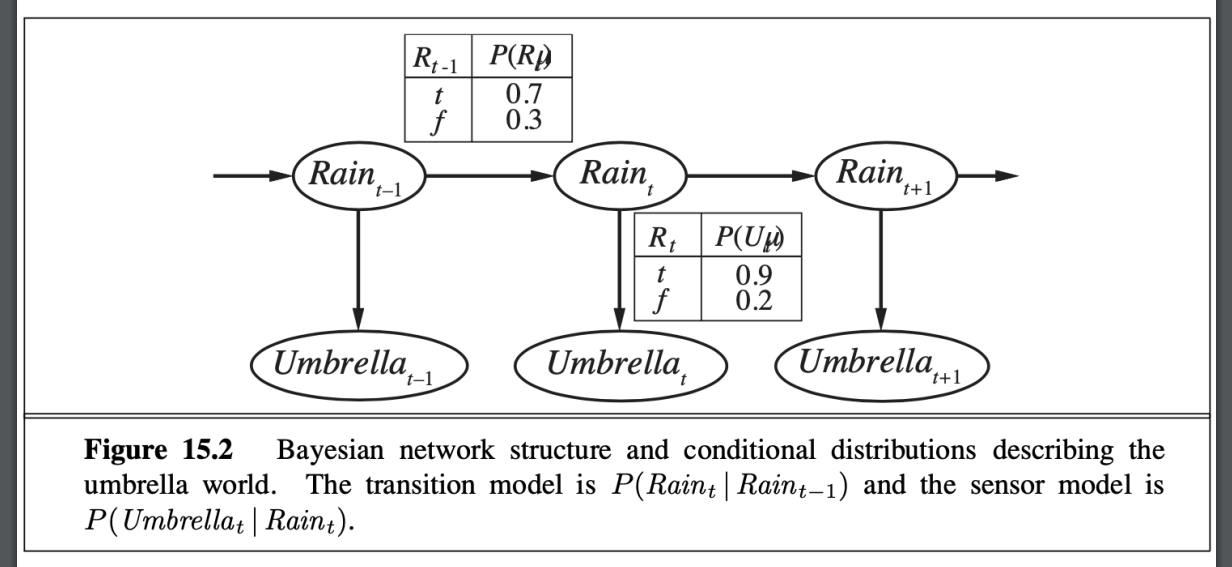
  • 圖像化

• 整個形式

  

  • initial state model
  • transition model
  • sensor model

• 假設正確與否 取決於該domain

  
  

  • 提高準確度的方法: 增加order 或是 添加更多變數

Inference in Temporal Models

• 濾波

  

  • 以過去到現在的狀態 找出跟當前有關的資料 推論現在的狀態

• 預測

  

  • 以過去到現在的資料 預測未來數個時間點的狀態

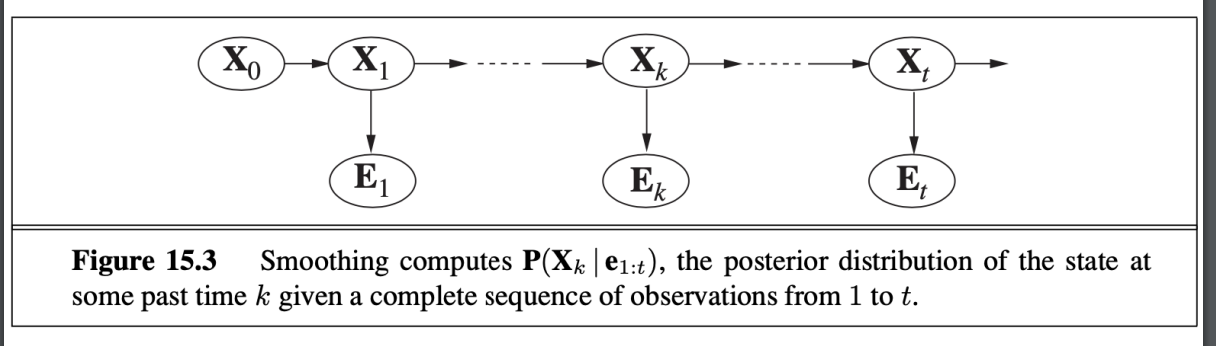
• 平滑

  

  • 以過去到現在的資料 推論過去的狀態

• 最大可能解釋

  

  • 找出一串環境狀態 能夠最大的去解釋 evidence

• 學習

  

  • 使用 EM algorithm

Filtering and prediction

• 透過函數更新當前狀態 減少回去找歷史資料的情況

  
  

  • 稱之為 recursive estimation

    

  • 藉由 conditioning 現在的狀態 繼續拆開等式 => 藉由當前的狀態 預測下一個狀態的機率分布

    

  • 將機率寫成 message的形式

• 雨天的例子 預測兩天

  
  

• Prediction

  

  • 其實就是Filtering 延伸到+k
  • 沒有證據版本的 => 所以只有 transition model

Smoothing

• 平滑的做法

  
  

• backward message

  

  • 反覆的transition 並藉由狀態預測evidence

    

  • 第一和第三個factor 都是model本身就有的
  • 第二個factor 就是recursive call

• 故得知f, b都可以靠 recirsive求得

  
  

  • 雨天計算的例子

• Smooth 的計算複雜度

  

• forward-backward algorithm

  

  • forward 由前往後
  • backward 由後往前
  • 並用表紀錄計算出來的值 減少計算複雜度

    

Finding the most likely sequence

• MLE

  

  • 用smooth 去找出後驗機率分佈

    

  • 像在走圖

    

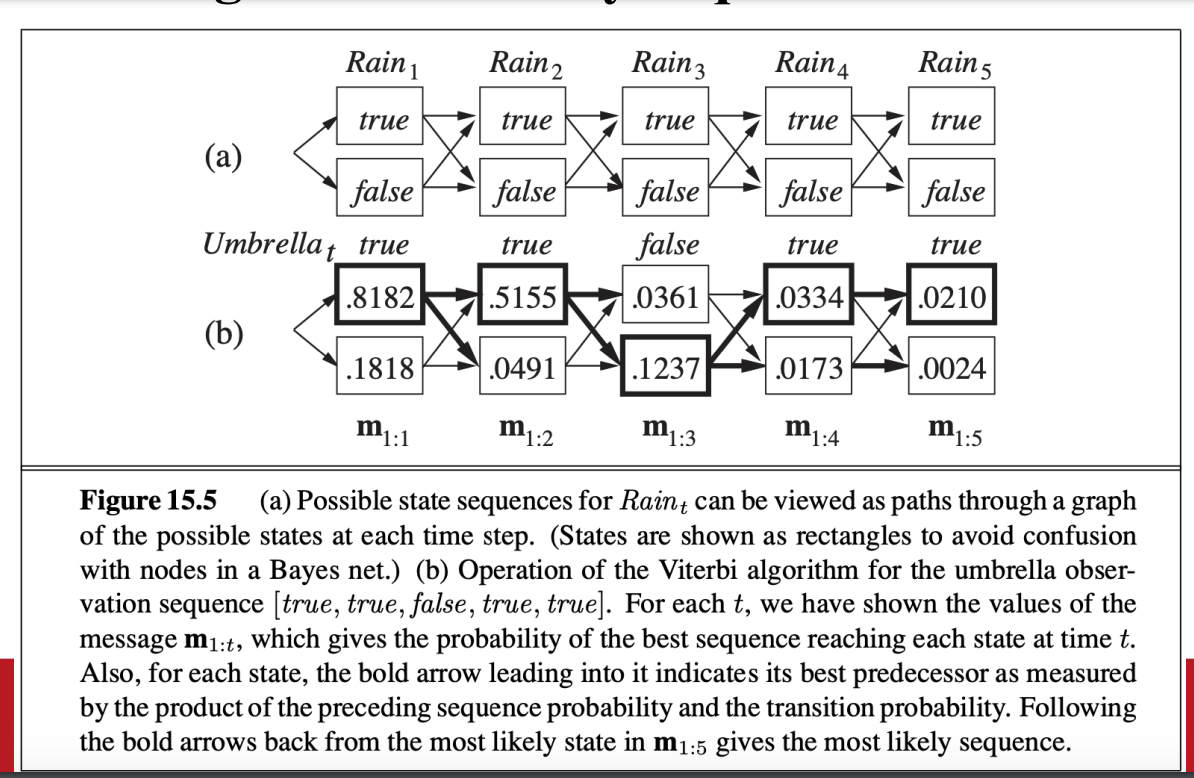
  • 選擇機率最高的 邊走邊smooth

• 當前的最可能路徑 與過去最可能路徑 以及當下證據有關

  

  • 基本上就是說明上面會對的核心思路是什麼

• 跟forward 的差別就只是message的不同

  

  • 形式是類似的

    

  • 所以本質上就是filtering

• Viterbi algorithm

  

  • 因為message的差別 跟filtering的時間複雜度一樣 但空間複雜度不同

Hidden Markov Models

• intro HMM

  

  • 解決離散問題

HMM example: Localization

• 吸塵器的例子

  
  

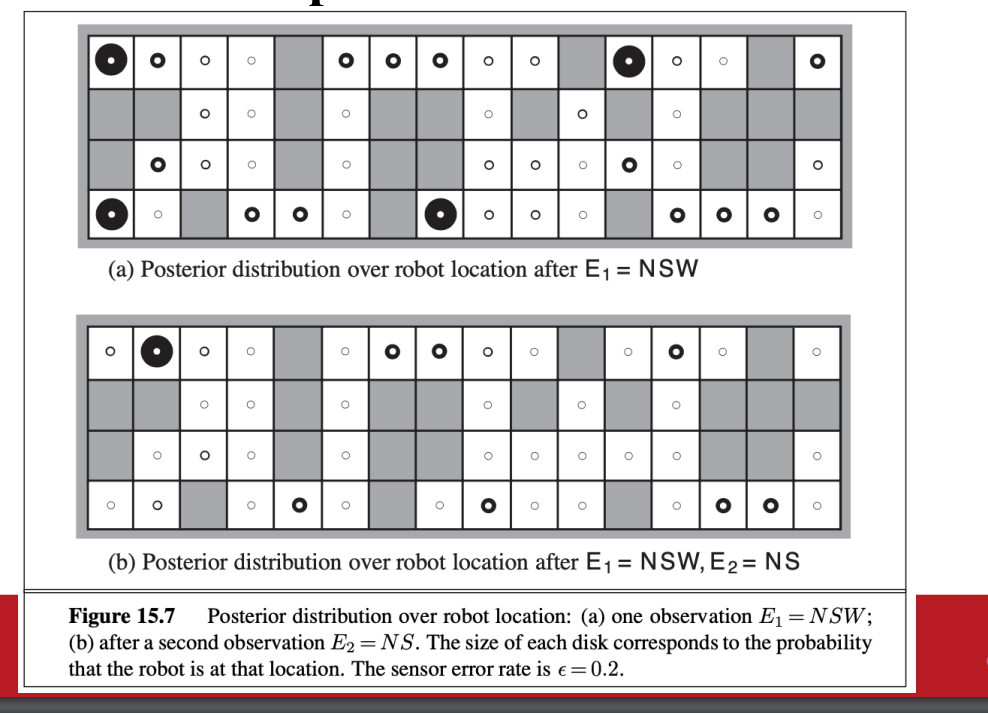
  • transition matrix的大小

    

• 為收集數據建立機率分佈模型

  
  

• 用sommthing 知道某個時間agent在哪裡 用viterbit algorithm 知道最有可能的路徑

  
  

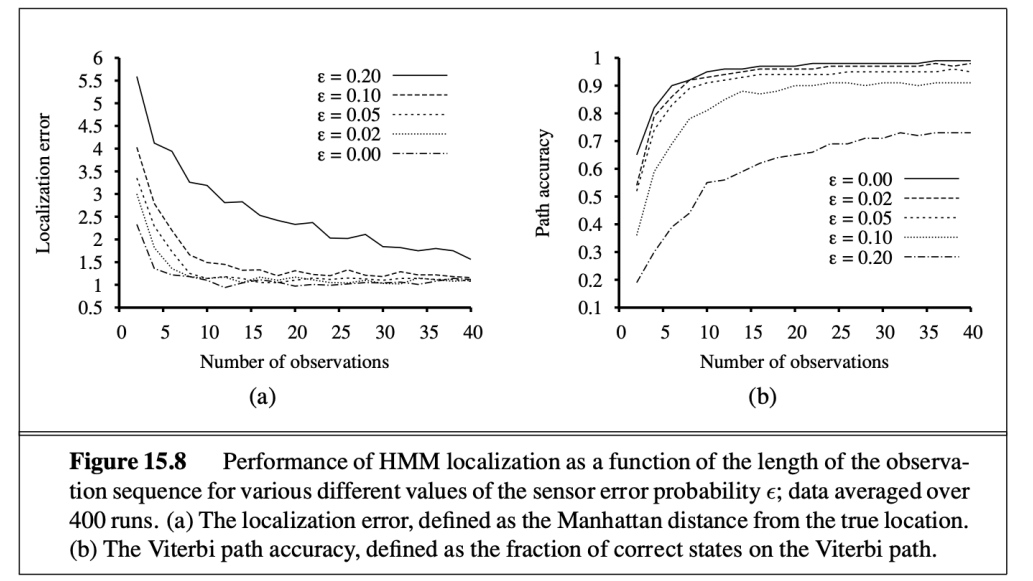
• 廣泛的說 能具備高等級的定位 以及準確路徑 即使是存在error的情況下

  

Kalman Filters

• 解決連續的問題

  

• 使用高斯建模

  

• Bayesian network

  

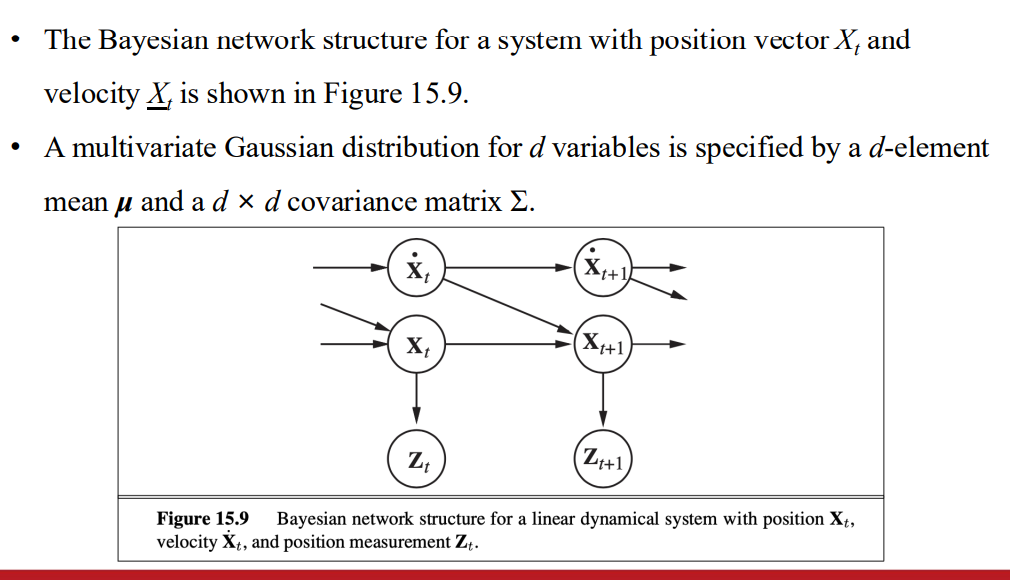
Updating Gaussian distributions

• 線性高斯之間 運算的封閉性

  

• 寫成forward的形式

  

A simple one-dimensional example

• 一維的例子

  
  

• 二次方程式能夠配方 因此補正項會獨立出來

  

  • 配方項則是e從負無限積到正無限 相當於1

• Bayer’s rule

  

  • 得出狀態的更新結果

• 結論

  
  

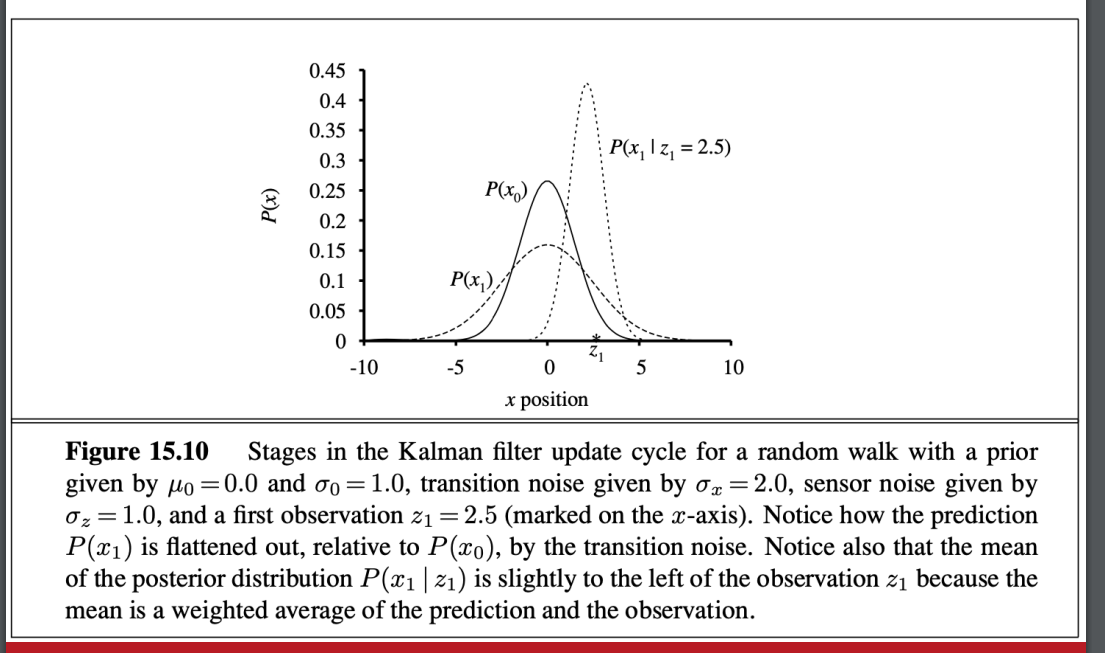
• 更新解釋

  

  • 平均值的更新 受到不確定性影響(變異數)
  • : 過去平均的不確定性
  • : 轉移過程的不確定性
  • : 觀察的不確定性

    

  • 方差的更新和 觀測值獨立 => 一種固定模式 可以提早計算
  • 方差會收斂 => 穩定衰減到固定值

The general case

• 對多元素向量 也是同理

  

• 定義transition model and sensor model

  
  

  • 如何更新 mean
  • K 代表要如何考慮觀測值的影響 (置信度 高or低)

• 例子

  
  
  

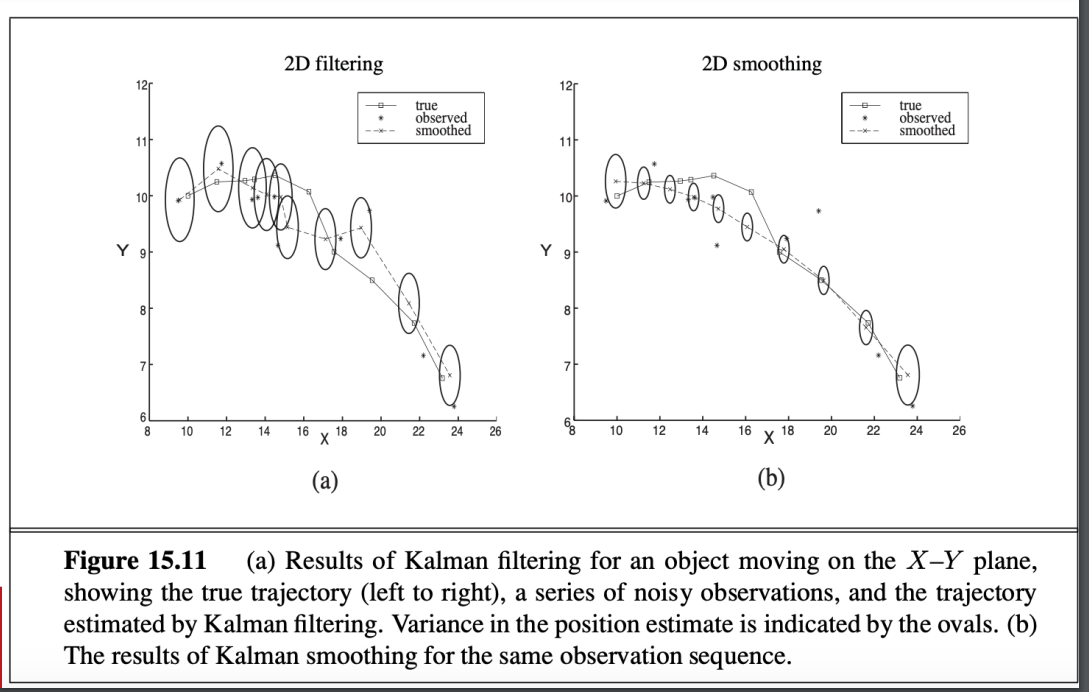
  • smoothing的公式 也可以推導

Applicability of Kalman filtering

• 應用範圍 任何連續的都可以吧

  

Keeping Track of Many Objects

• 多物體給出的觀察

  

  • 不確定性：我們無法確定每條觀測數據是由哪個物體產生的。
  • 可能性增加：每個觀測值都可能來自於任意一個物體，導致需要考慮多種數據分配情況。

• 空難的例子

  
  
  

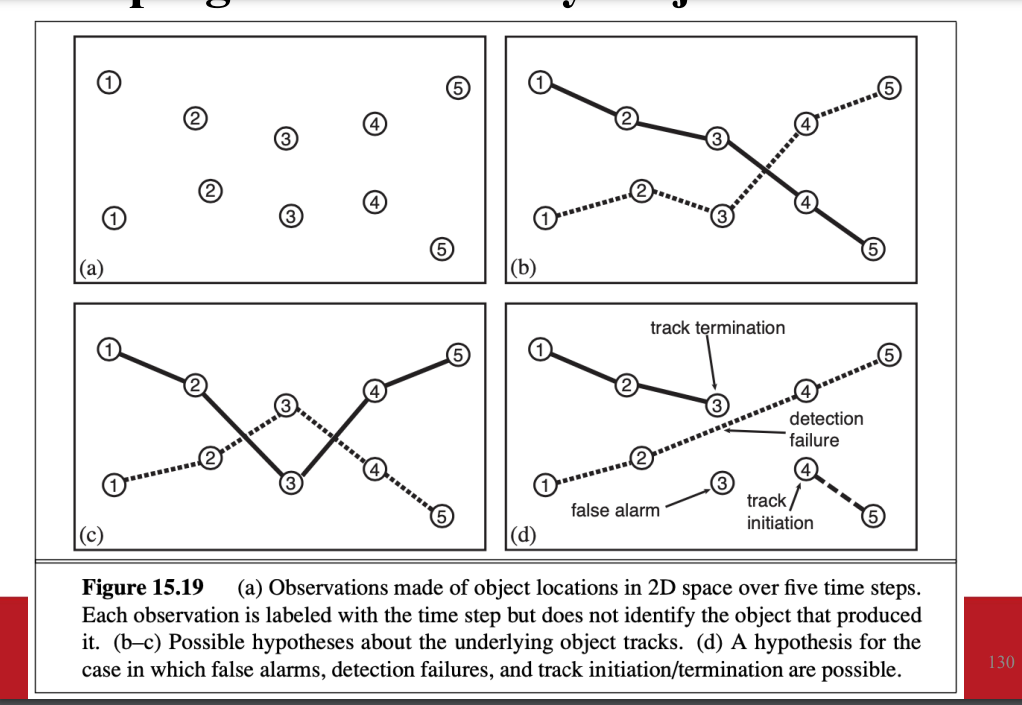
  • 整理形式後

• 無法分辨觀測來源的話 問題會極度複雜

  
  

  • 一對一映射 來簡化問題

    

  • 簡化

• 對這個問題 可惜還沒有有效的算法可以解決

  

• 估計方法

  

  • 每個時間戳 選一個最好的
  • nearest-neighbor filter

    

  • 最大化 joint probaility
  • Hungarian algorithm
  • n! 種選擇

    

  • particle filtering
  • 維護很大的 可能選擇的集合

    

  • MCMC (Markov chain Monte Carlo)
  • 探索分配的歷史空間 隨機抽樣這些可能的分配
  • 而且可以在探索中隨機轉移分配狀態