Chapter 19 Learning from Examples
Chapter 19 Learning from Examples
Introduction
- Agent learning

Supervised Learning
監督式學習

分類與回歸任務
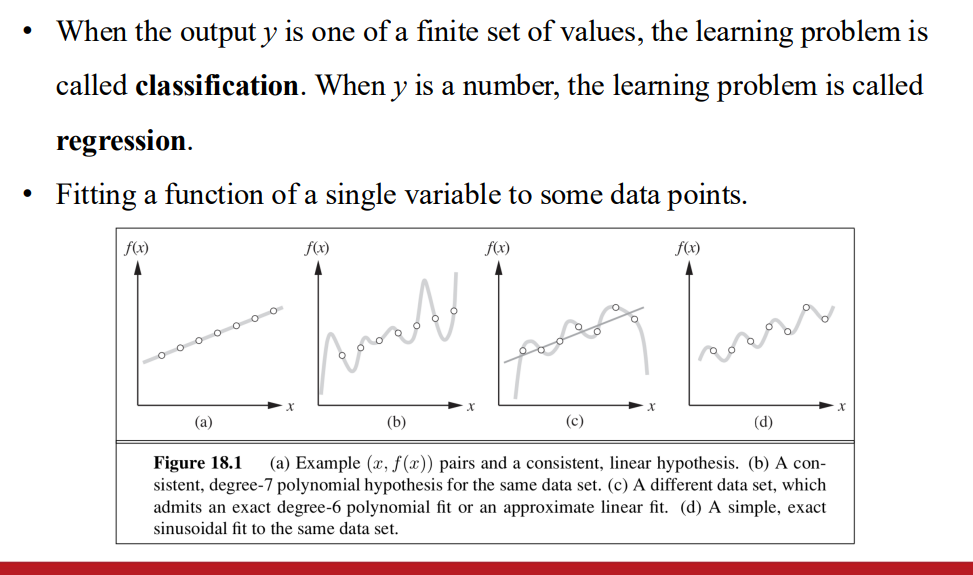
Ockham’s razor

- 選擇與Data一致 且最簡單的形式
learning problem 是可實現的 如果假說空間存在真實的答案

- 權衡
- 複雜的假設 可能在訓練資料表現更好 但在未見過的資料效果差
- 簡單的假設 可能更具有泛用性
- 權衡
使用Bayer’s rule簡化

- 低次多項式: 更泛用 對假設的可信任度高
- 高次多項式: 可能overfitting 對假設的可信任度低
: 對假設的可信任度
另一種權衡

- 假設空間的表達性 vs. 在該空間找到好假設的複雜性
Learning Decision Trees
學習決策樹

問題定義

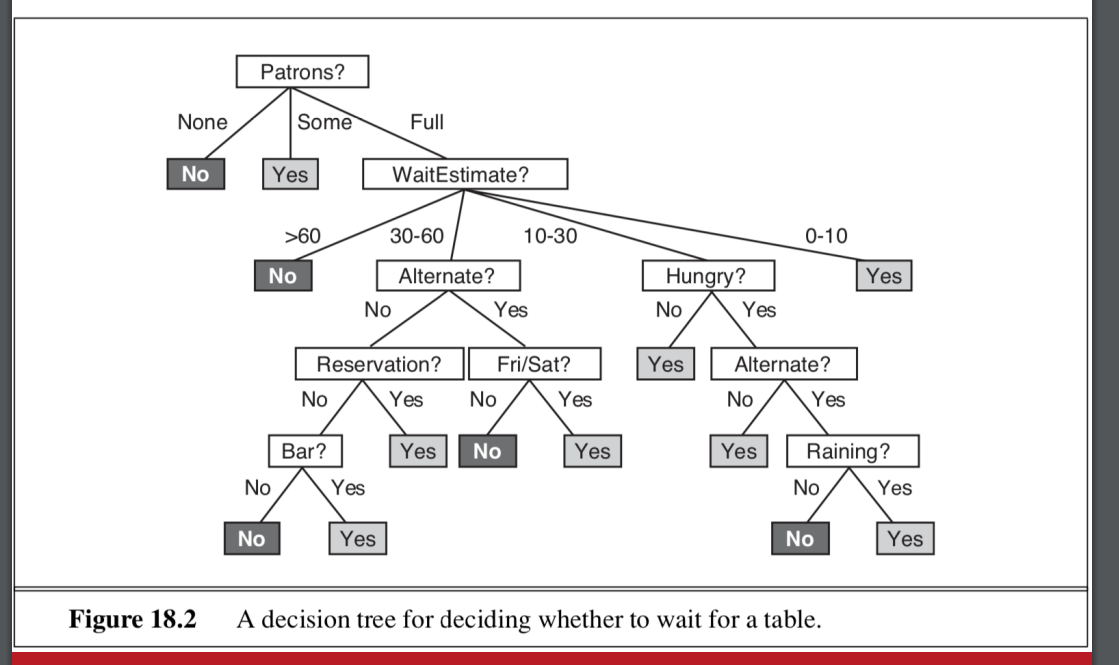
- 樹的長相

- 樹的長相
簡化問題

- 優先決定影響力大的項
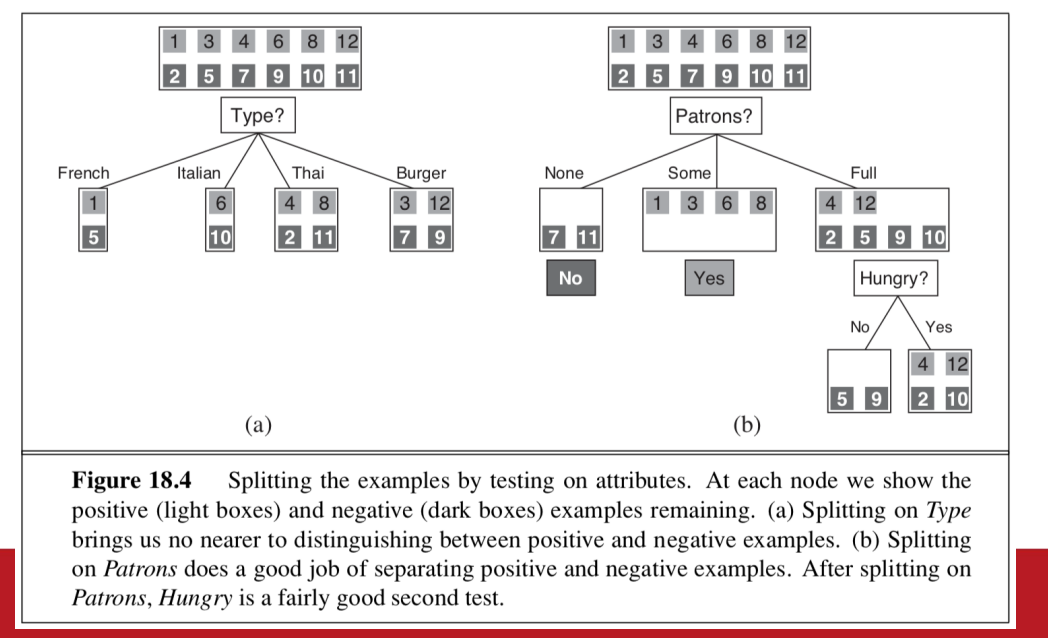
- type較差 因為他分出來的結果 每一項的正負樣本數量一樣

- 優先決定影響力大的項
子樹也是決策樹

標籤測試 對應於熵的測量

- 一個公平硬幣 相當於1bits的熵

- 公式 以及實際計算的例子

- general form
- 目標屬性的熵表示在沒有任何額外資訊的情況下,數據集的混亂程度。
- 當正負例均勻分布時,數據集的不確定性達到最大值,需要 1 bit 的信息來進行完全區分。
- 一個公平硬幣 相當於1bits的熵
如何選出影響力高的標籤

- 計算孩子們的熵總和

- 比較information gain: 越高代表得到的資訊越多 => 把樣本區分的越清楚
- 計算孩子們的熵總和
generalization and overfitting
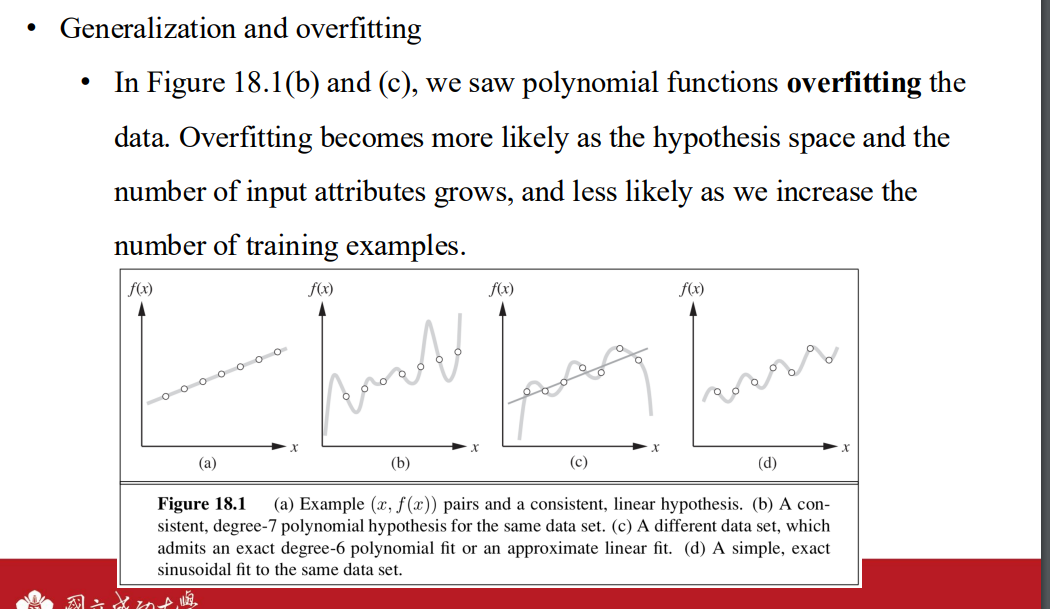
- 當假設空間變得更大(例如,允許更高次的多項式)時:
- 模型擬合訓練數據的能力增強。
- 但模型更容易記住訓練數據中的噪聲,從而導致過擬合。
- 當輸入特徵(attributes)數量增加時,模型變得更複雜:
- 更多的特徵可能包含與輸出無關的噪聲。
- 模型可能會過於依賴某些特徵組合,導致過擬合。
- 特徵選擇的重要性:
- 篩選出真正相關的特徵可以減少過擬合。
- 過多無關特徵會增加假設空間的大小,使模型更容易過擬合。
- 當訓練數據量增加時:
- 每個假設需要解釋更多的數據點,模型更難專注於噪聲。
- 訓練數據的多樣性更高,有助於模型學習到數據的普遍模式,而非特定的樣本特性。
- 關鍵觀察:
- 訓練數據量越多,模型越能抵抗過擬合。
- 增加數據量是緩解過擬合的有效手段,但可能伴隨更高的數據收集成本。
- 當假設空間變得更大(例如,允許更高次的多項式)時:
拓展決策樹的應用

- 如果輸入是連續的 => 分段
- 如果輸出是連續的 => 使用regression tree 而非 decision tree
有廣泛應用 優點是人知道導致輸出的原因

Evaluating and Choosing the Best Hypothesis
example: independent and identical distributed


- 平穩性假設: 訓練數據與測試數據來自於相同的分佈
- 獨立同分佈(IID)假設:
- 樣本之間是相互獨立的(independence),即後續樣本的生成不受之前樣本的影響。
- 所有樣本具有相同的先驗概率分佈(identical distribution),這是機器學習模型訓練的基礎。
- 透過平穩性假設和 IID 假設,我們可以將數據視為一個隨機樣本集合,這是大多數機器學習理論的基石
- 能夠更好的適應未來資料
error rate

- 低訓練錯誤率≠良好的泛化能力:
- 模型在訓練數據上的低錯誤率,不能保證其在未見過的測試數據上也有相似表現。
- 這種現象可能由於過擬合(overfitting)導致,模型過於適應訓練數據中的細節或噪聲,失去泛化能力。
- 低訓練錯誤率≠良好的泛化能力:
k-fold cross-validation

- 也稱之為 leave one out cross validation => LOOCV
peeking 偷看

- 當訓練人員 根據測試集的分數來 設置假設的時候 => 測試集的資訊被洩漏出去了
validation dataset

model choosing

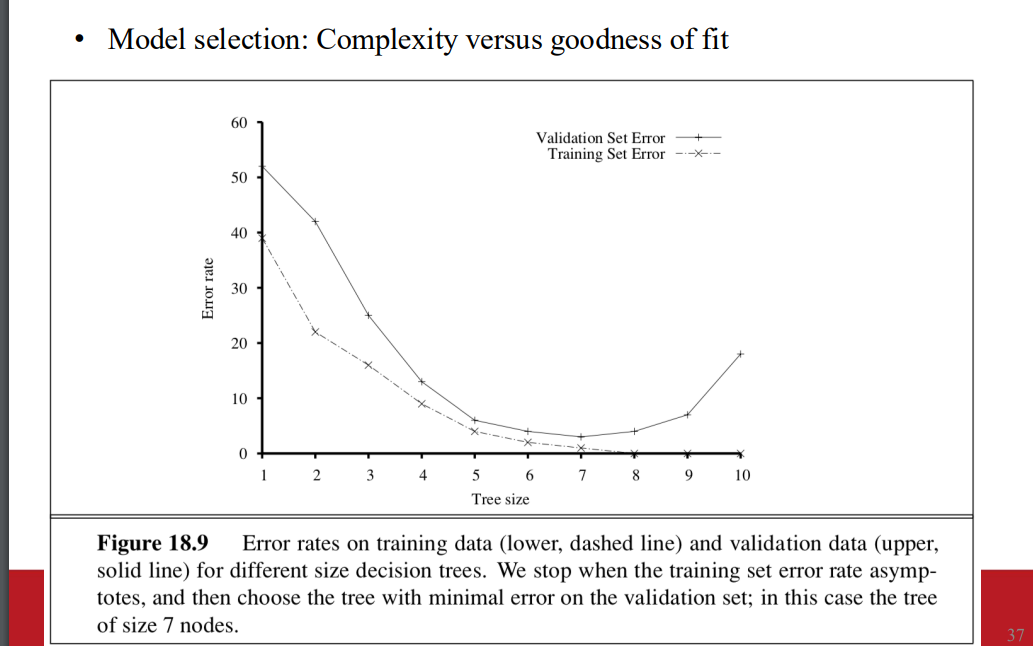
loss function


加入先驗機率


- 因為agemt 不知道先驗機率 所以只能取1/N => empirical loss 經驗損失
正規化

- 加入對於方法複雜性的懲罰
Regression and Classification with Linear Models
單變數線性回歸

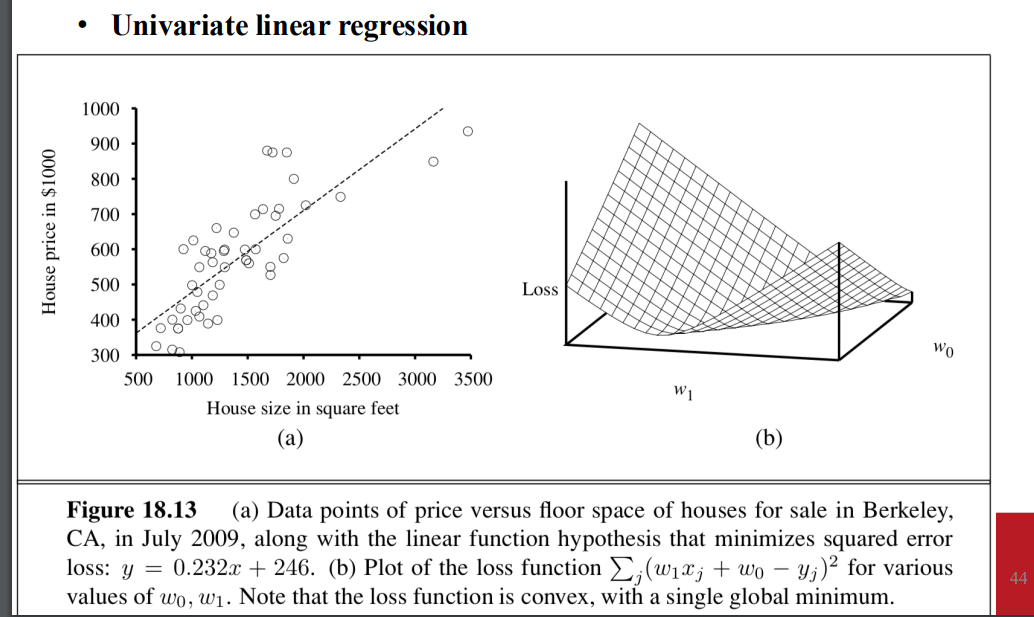

- 最小化loss 就是找出對
, 取導後等於0的解 - 可以直接找到

- 權重空間 2維的 => loss function is convex 所以沒有local minima
- 最小化loss 就是找出對
離開線性模型

- loss function 沒有解 => using hill climbing
學習率


- 實際微分的長相
批次梯度下降

機率梯度下降 Stochastic gradient descent

多變數線性回歸


- 梯度下降 可以找到唯一的最佳解
closed answer



regularization

L1 regularization 可以產生稀疏模型設置閾值可以用於分類

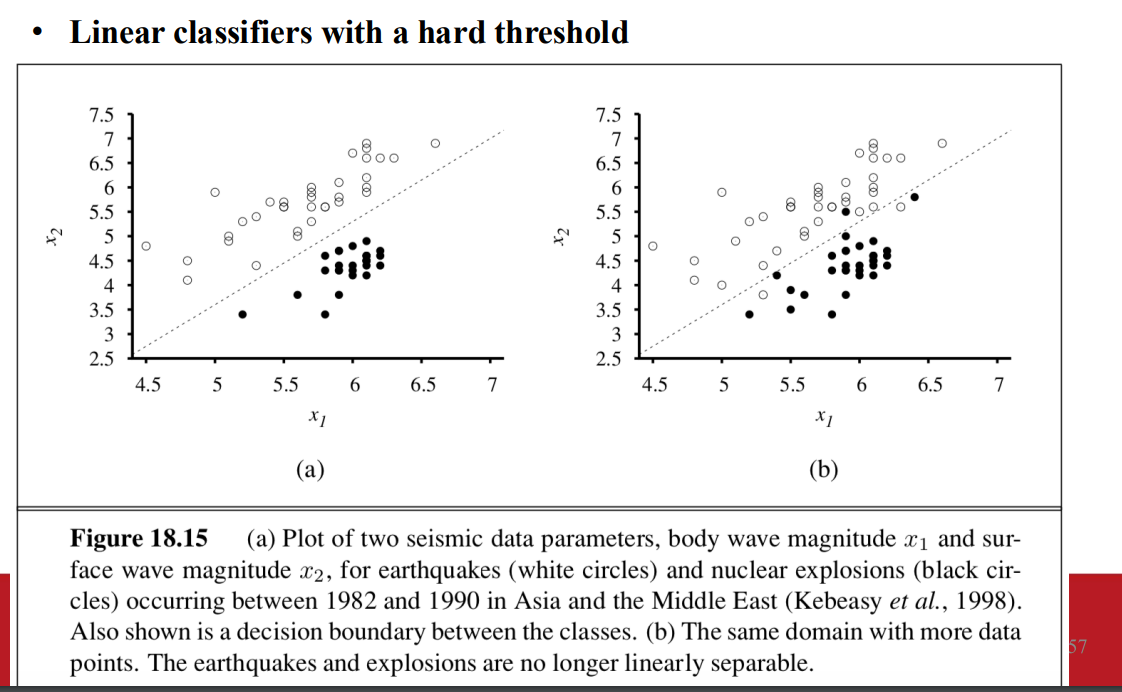
- hard threshold
decision boundary

- 一條線 或是介面可以分出資料的類別
- 資料如果具備能分類的特性 => linearly seperable

- 更新形式 linear regression的單變數導數形式
- perceptron learning rule 感知器學習原則

- 三種可能的改變
每次在同一個訓練集更新後的結果


- perceptron rule 可能不會收斂到穩定的解 (固定學習率下)
Softening the hard threshold function

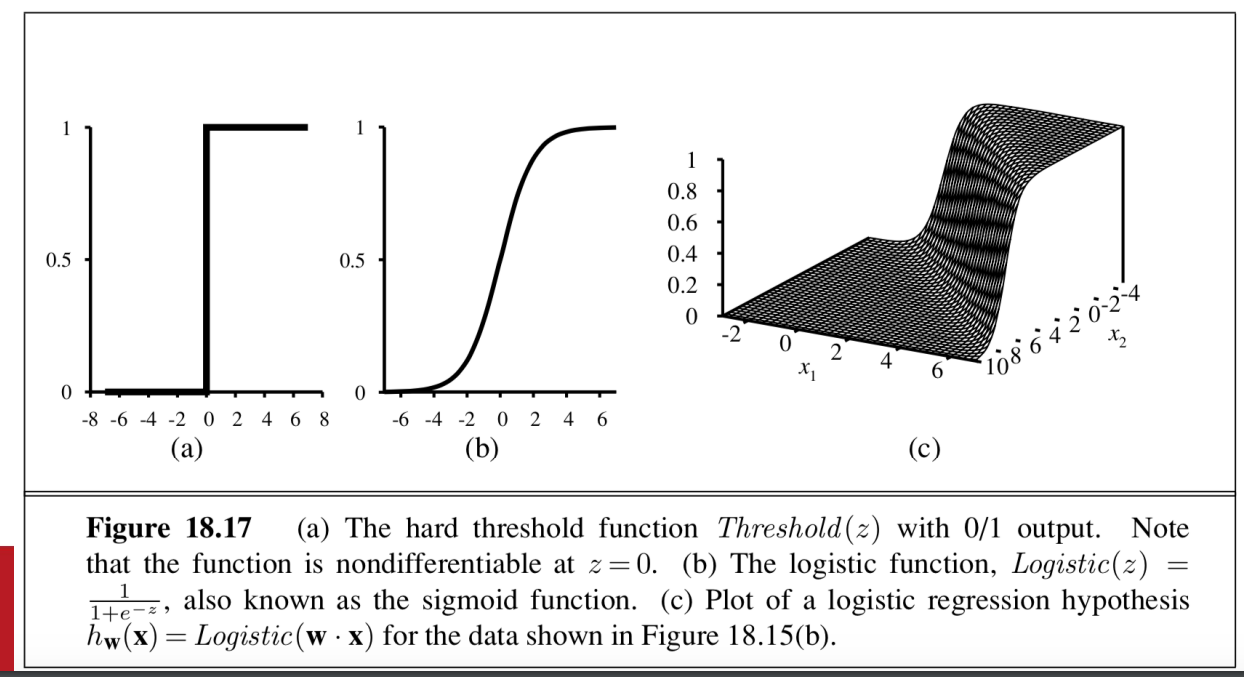
- like sigmoid function

- 輸出介於 0~1之間 可以視為預測結果為類別1的機率
- like sigmoid function
logistic regression

- 沒有封閉解
- 可以使用 gradient descent

- 使用chain rule 推導gradient
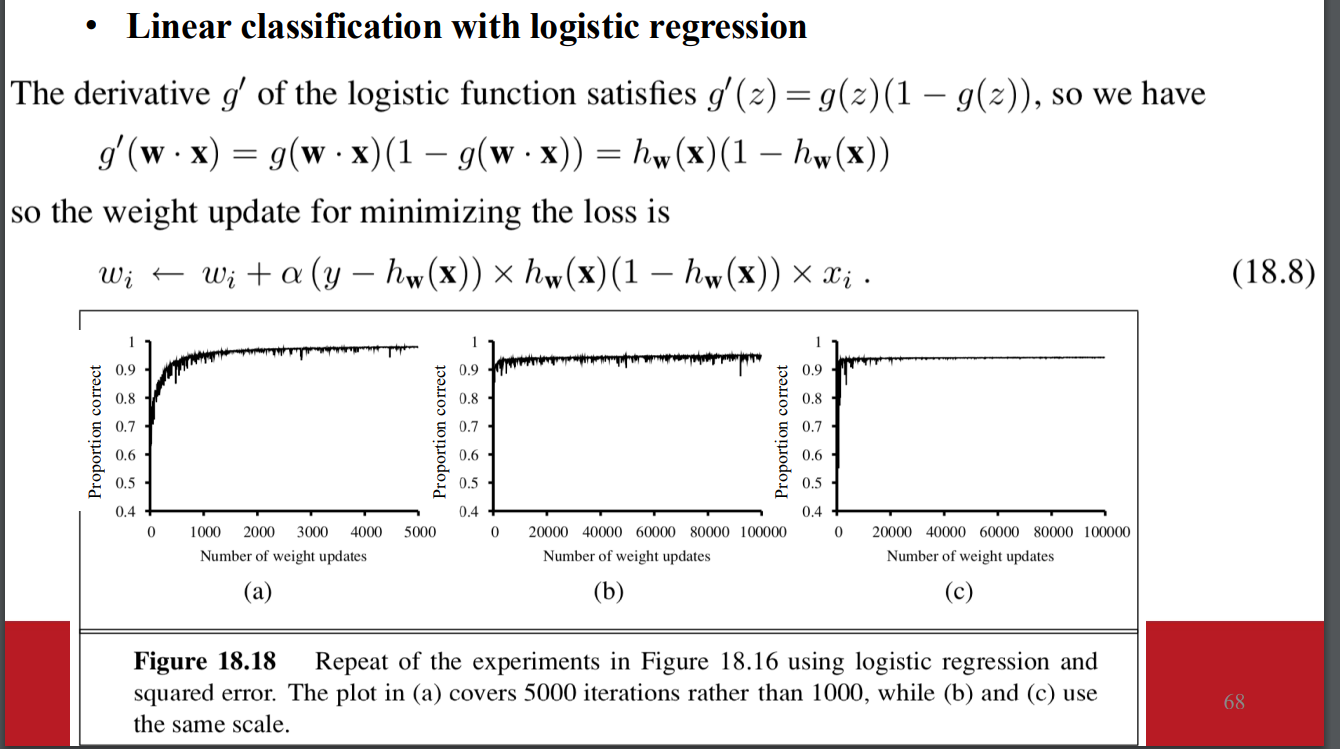
- 梯度更新公式
Nonparametric Models
parametric vs. nonparametric

- Parametric: 只記錄最終的函數 不包含訓練資料
- Nonparametric: 還需要訓練資料來幫助預測
instance-based learning or memory-based learning

- table lookup
KNN

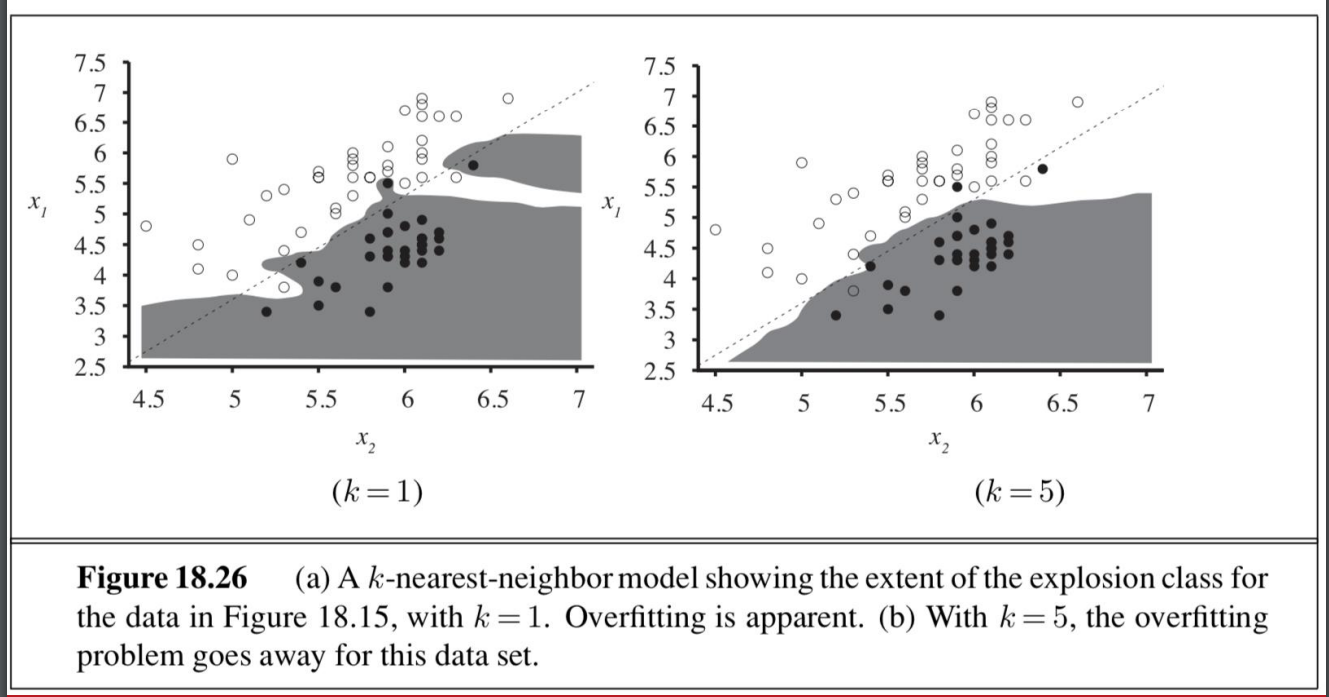
- 不同k值的例子

- nonparametric model 也會有overfitting的問題
- 通常用cross-validation 來找出最佳的參數
- 不同k值的例子
distance metric

- Minkowski distance
- Euclidean distance
- Manhattem distance
- 對於布林標籤: Hamming distance

- 標準化
- Mahalanobis distance考慮到不同維之間的關係 (馬哈拉諾比斯距離)
在高維空間下KNN的稀疏性



- 維度越高 鄰域越接近整個空間的大小

- 維度詛咒
- 維度越高 鄰域越接近整個空間的大小
K-d tree

- 重覆在特定維度上 把資料分成兩半


- 數據量要求 如果數據不夠 效果不如線性掃描好
- 重覆在特定維度上 把資料分成兩半
Locality-sensitive hash (LSH)

- 局部敏感哈希

- 能處理最近鄰問題 但仍舊存在高維詛咒


- 找出能反映距離的hash function


- 作法
- 用hash table找出相近的候選 再做k-neighbor
- 局部敏感哈希
折線圖
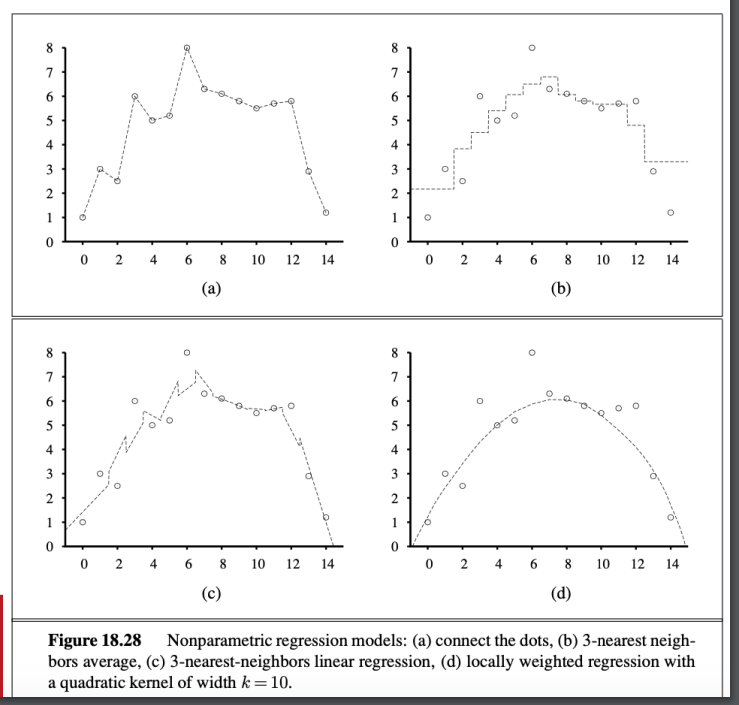
回歸


- weight kernal
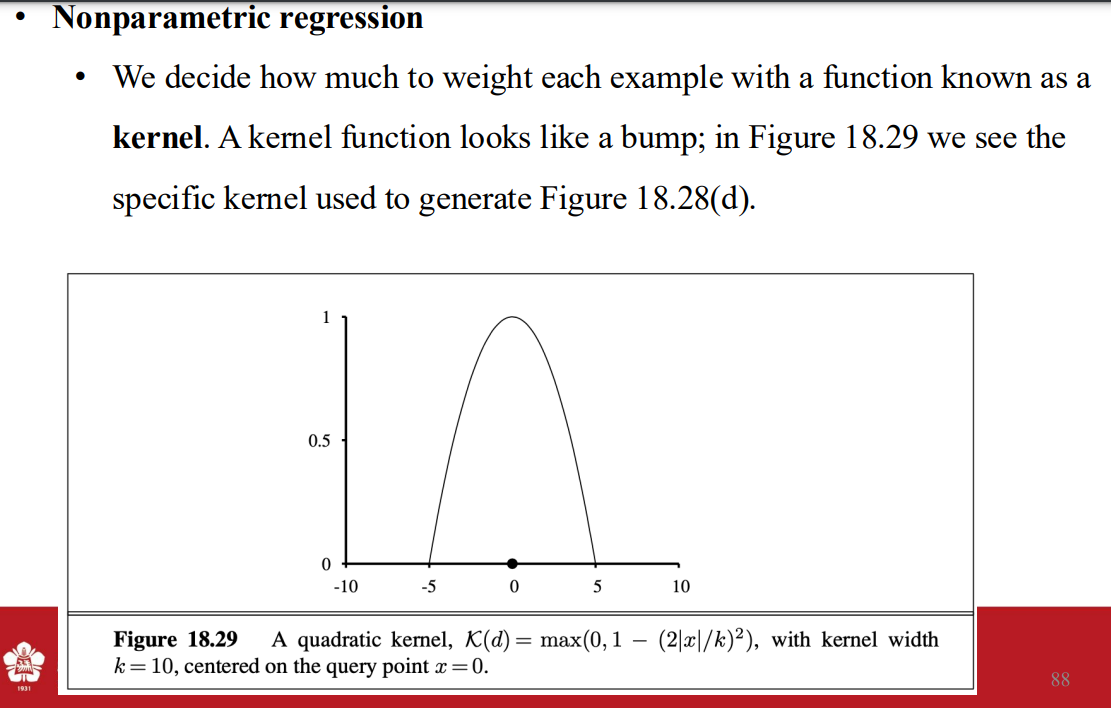
- locally weighted regression

- weight kernal
Support Vector Machines
SVM

- 現成方法 尤其是在沒有相關領域知識的情況下
- 最大邊緣分割器
- 使用 kernal trick的技巧
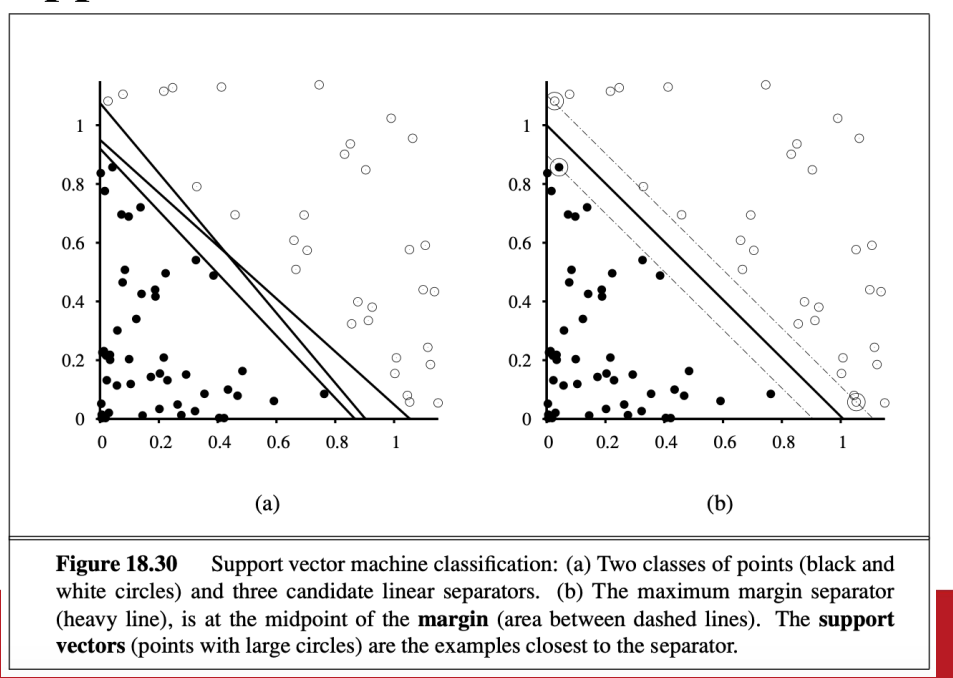
某些樣本更重要 放更多注意力在這上面 可以增加泛化性

比起關注經驗損失 更關注預期的泛化損失

- margin: 從 separator 到最近點的距離 這個範圍

- 解方程式(separator) => 最大化margin
- margin: 從 separator 到最近點的距離 這個範圍
quadratic programming problem


- 轉換後的方程式有幾個好處
- convex => 有全域最小解



- convex => 有全域最小解
- 轉換後的方程式有幾個好處
資料如果不能線性分割 => 引入高維空間
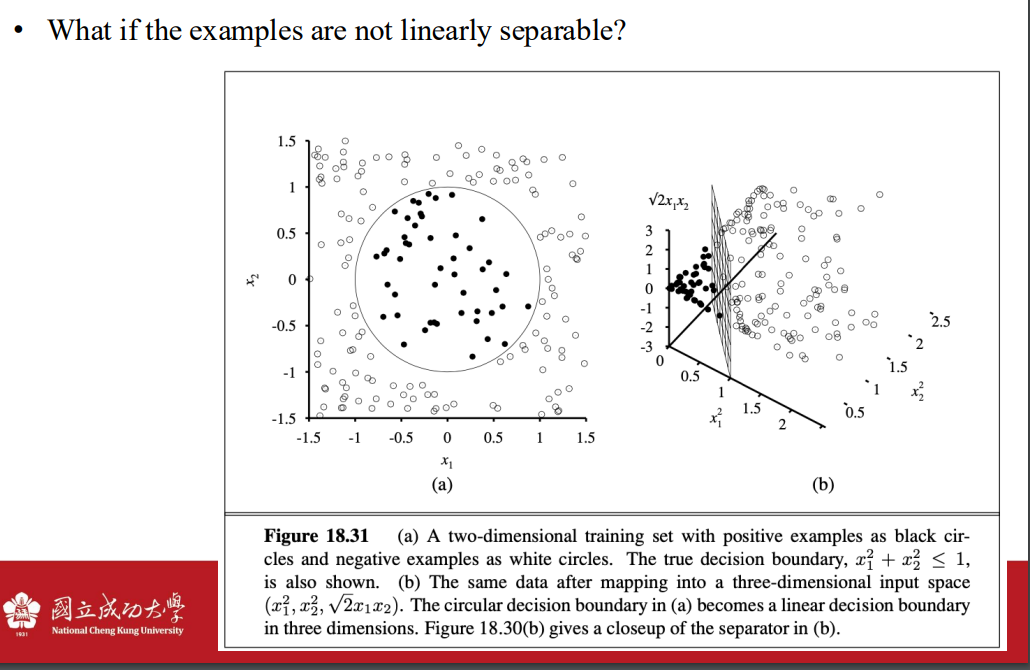
- 自己定義函數


- 操作方法

- 只要計算kernal function 就好

- 使用這些kernal function => kernal trick
- 自己定義函數
軟邊界向量機

- 允許錯誤分類: 不要求所有點都在正確的分類區域。
- 懲罰錯誤: 對於那些落在錯誤一側的樣本,其懲罰與將其移回正確區域所需的距離成正比。
Ensemble Learning
- ensemble


Ensemble Learning – Bagging
- 將資料拆成k份 訓練出k個變體

Ensemble Learning – Random forests
- 隨機森林 種出一堆不同的樹


- 越多樹 誤差會收斂
Ensemble Learning – Stacking
- 推疊不同模型的成果到驗證集


- 再使用驗證集訓練最終的模型
Ensemble Learning – Boosting
boosting

- 權重越高的example 越重要

- 從所有人權重都一樣開始
- 提高錯誤者的權重 降低正確者的權重 重新訓練變體
- 將所有變體的結果結合
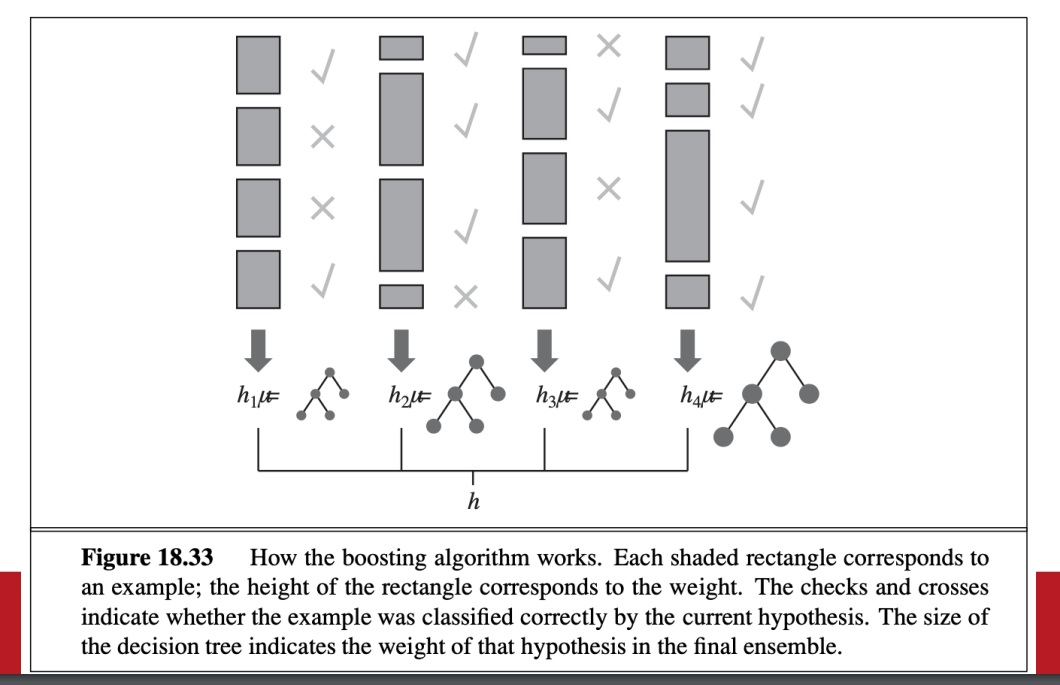
- 權重越高的example 越重要
Adaboost


- 集成弱學習器形成強學習器:
- AdaBoost 是一種提升演算法 (Boosting Algorithm),透過結合多個弱學習器(例如簡單的決策樹或樸素貝葉斯)來形成一個 強學習器。
- 強學習器的性能遠高於單個弱學習器。
- 提高訓練集準確率:
- 如果給定的弱學習演算法在每次迭代中都能生成準確率略高於隨機猜測的假設,AdaBoost 通過多次疊加這些假設,會逐漸提升整體的分類能力。
- 理論上,當迭代次數 K 足夠大時,AdaBoost 可以將訓練集的分類錯誤率降到 零,也就是訓練數據可以被完全正確分類。
- 集成弱學習器形成強學習器:
結果差異

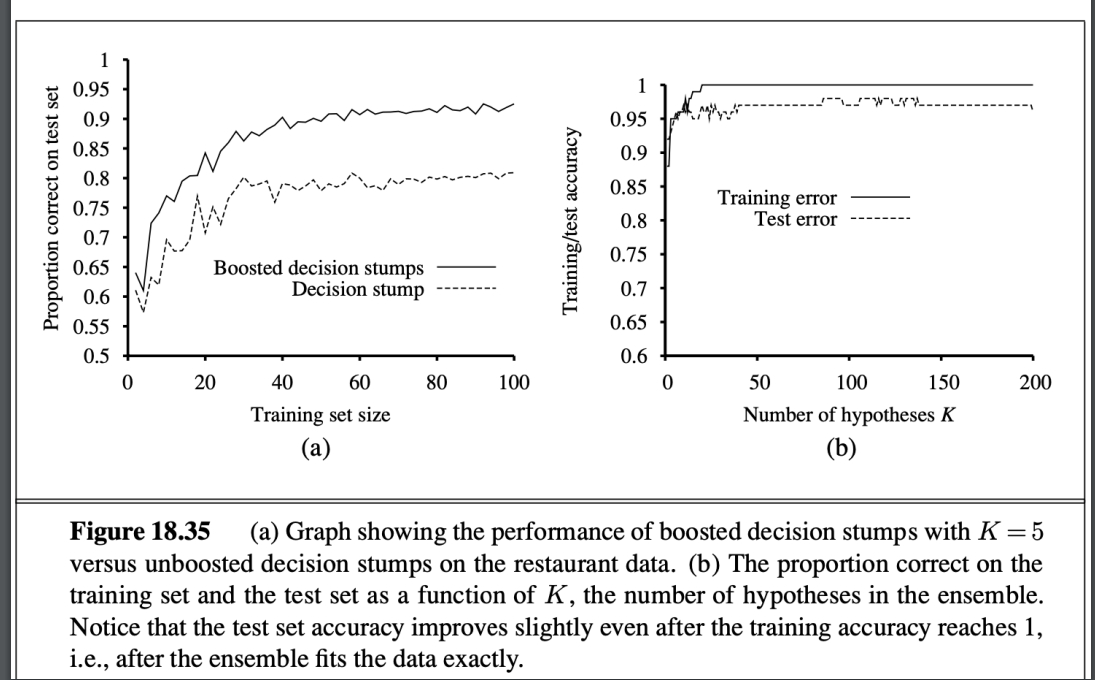
K值差異

Ensemble Learning – Online learning
很強的假設 未來的資料很難跟過去訓練的資料完全獨立

在線學習

隨機加權多數演算法

- 相信專家們的水平與過去表現成正比

- 作法
- 相信專家們的水平與過去表現成正比
根據regret變強

- regret: 遺憾 與最佳專家相比 我們犯下的錯誤

- 目標是最小化遺憾
- regret: 遺憾 與最佳專家相比 我們犯下的錯誤
Developing Machine Learning Systems
問題表述

資料收集

- 防止異常值
特徵工程

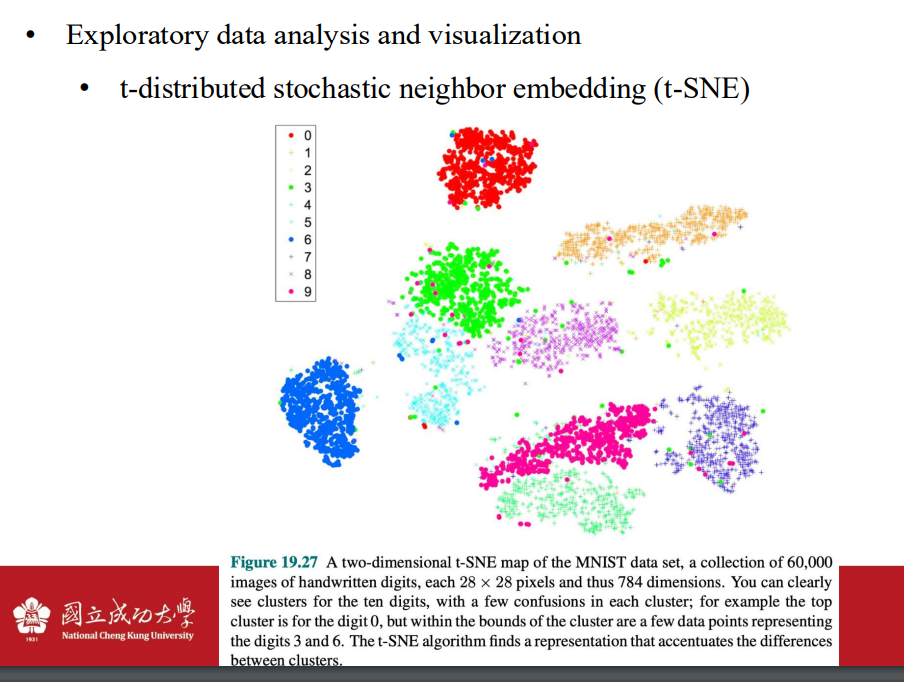
- 資料視覺化 用於去除異常值
模型選擇的baseline


可解釋性 與 可解釋能力

- 可解釋性 (Interpretability)
- 模型是 可解釋的,表示我們可以直接檢視模型的結構(如權重、規則、分支)並理解它的內部運作。
- 可解釋性通常與 簡單模型 相關,例如線性回歸或決策樹,因為它們的運算過程是透明且容易理解的。
- 可解釋性 (Interpretability)
- 模型是 可解釋的,表示我們可以直接檢視模型的結構(如權重、規則、分支)並理解它的內部運作。
- 可解釋性通常與 簡單模型 相關,例如線性回歸或決策樹,因為它們的運算過程是透明且容易理解的。
- 可解釋性 (Interpretability)