Chapter 20 Learning Probabilistic Models
Chapter 20 Learning Probabilistic Models
Statistical Learning
糖果的例子
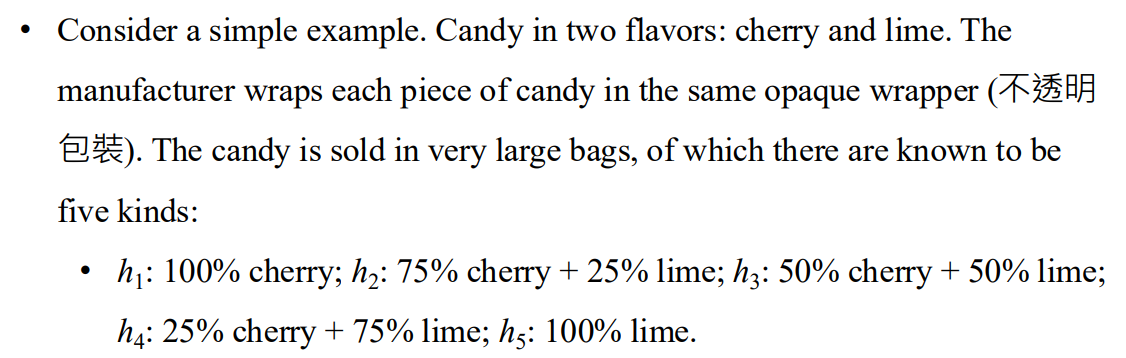

- 問題表述
Bayesian learning


- 預測公式
- 關鍵是過去的假設 以及在該假設下資料的可能性
計算假設下資料的可能性

條件機率隨著觀察到的數據改變 並轉移假說

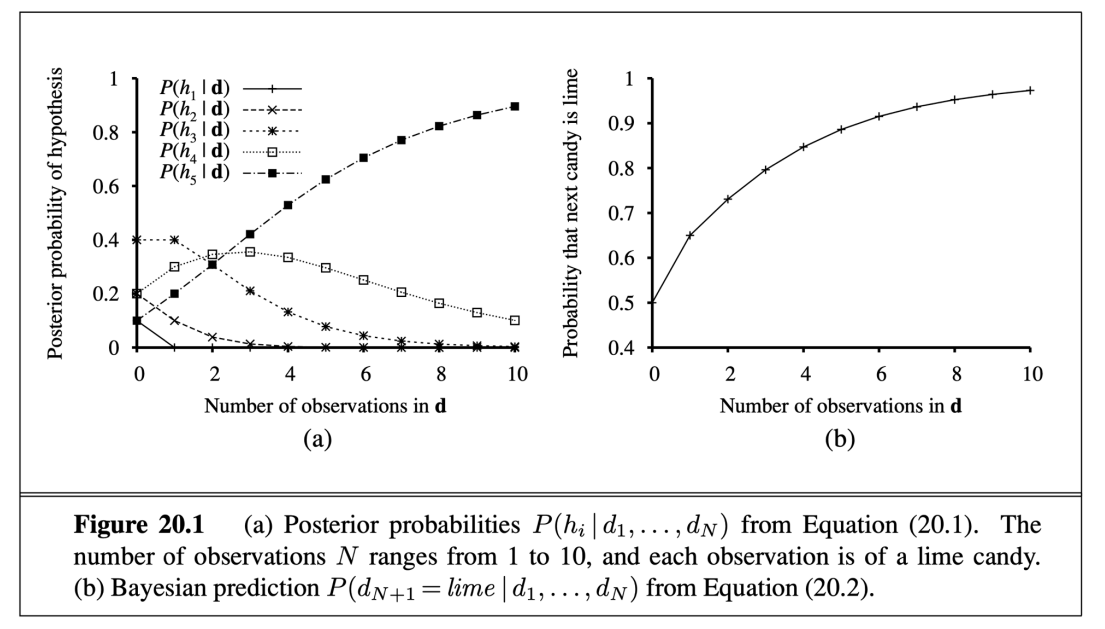
特性說明

- 特性描述:
- 貝葉斯學習的預測最終會收斂到 真實的假設,即使初始的假設先驗分佈不是完全準確的。
- 條件:
- 初始的先驗分佈不能完全排除真實假設。
- 隨著數據量的增加,模型可以逐漸識別出真實假設。
- 為什麼這會發生?
- 錯誤假設的後驗概率會隨著數據的累積而消失。
- 原因是:
- 如果某個假設是錯的,那麼它生成「不符合真實分佈特徵的數據」的概率會非常小。
- 當越來越多的數據被觀測到,這些數據越來越傾向於支持真實假設,而非錯誤假設。
- 特性描述:
maximum a posteriori (最大化後驗機率)

- 基於一個最可能的假設來預測

- MAP 比 bayesian 更容易實現
- 解決最佳化問題 比大型求和問題簡單
- 基於一個最可能的假設來預測
overfitting

- 使用假設的先驗機率 來懲罰假設的複雜性
Maximum-likelihood hypothesis



- 如果假設空間夠均勻
Learning with Complete Data
- 複雜資料

- density estimation: 密度估計 就是這種任務的名稱
- 專注於參數學習
Maximum-likelihood parameter learning: Discrete models
參數說明


- 針對該資料集的可能性
解ML的公式

- 實際的糖果分佈 跟已經被揭露出來的糖果分佈相同
模型圖
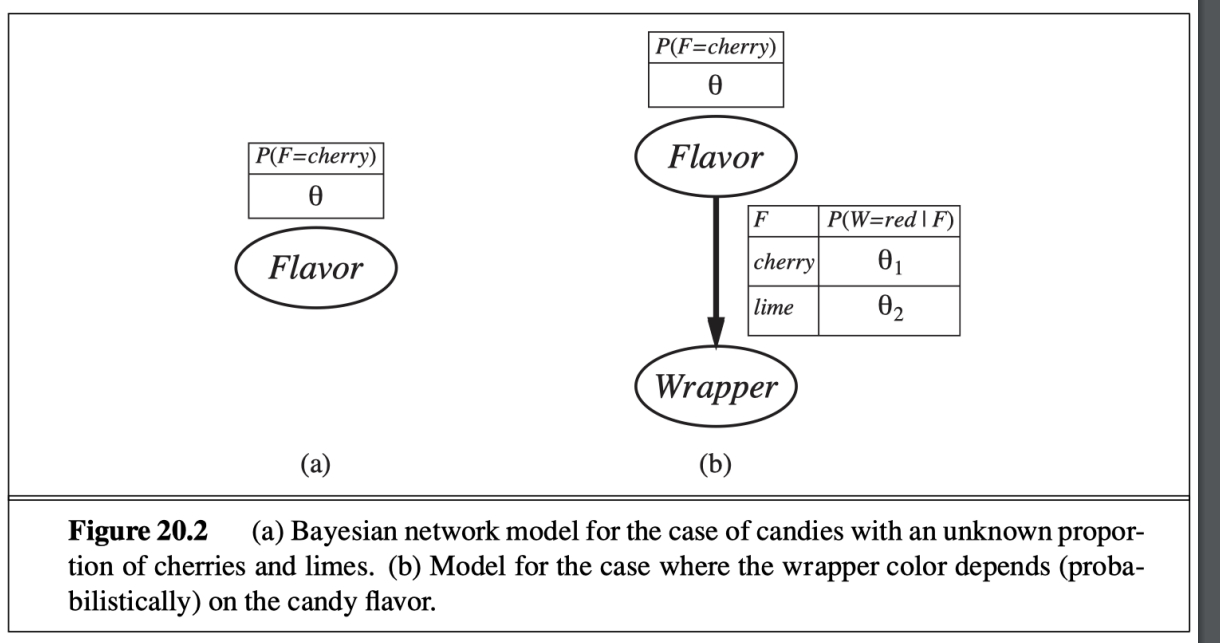
ML的解法說明


- 其他問題 比如說樣本數不夠
加入糖果包裝紙顏色的問題


- 看起來複雜 取log可以簡化

- 之後取導 可以變成三個獨立的項 方便計算
- 看起來複雜 取log可以簡化
Naive Bayes Models
天真的貝氏模型

- 假定每個標籤互相都是條件獨立的
當類別數量無法觀測 可以用這招

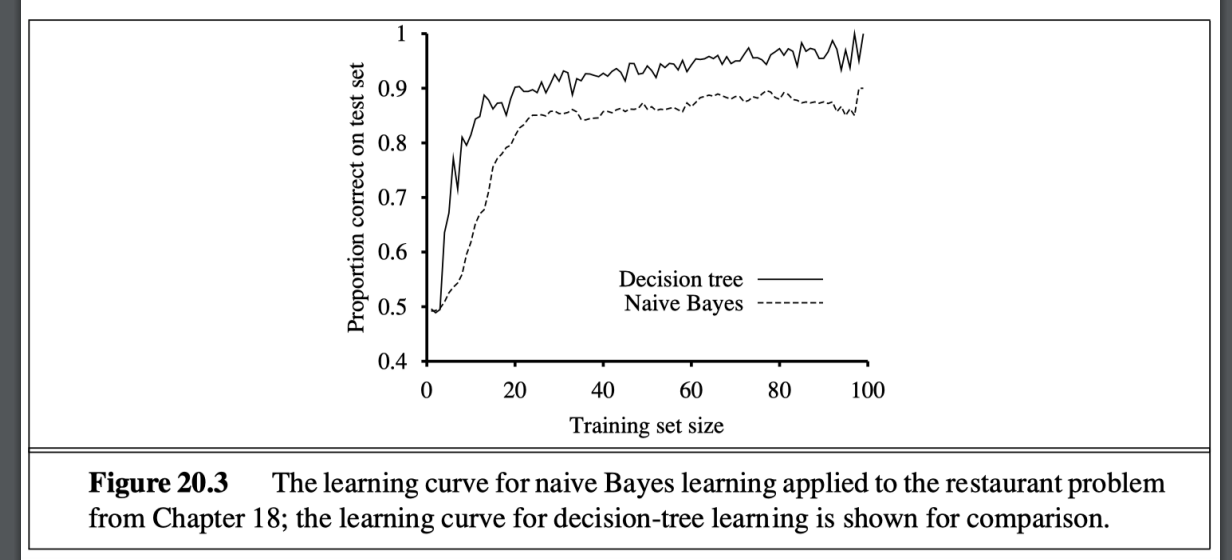
- 與決策樹的比較

- 主要的缺點是 條件獨立的假設很少是精準的
- 與決策樹的比較
Maximum-likelihood parameter learning: Continuous models
高斯分佈


- 解公式 找出Maximum likelihood
線性高斯模型

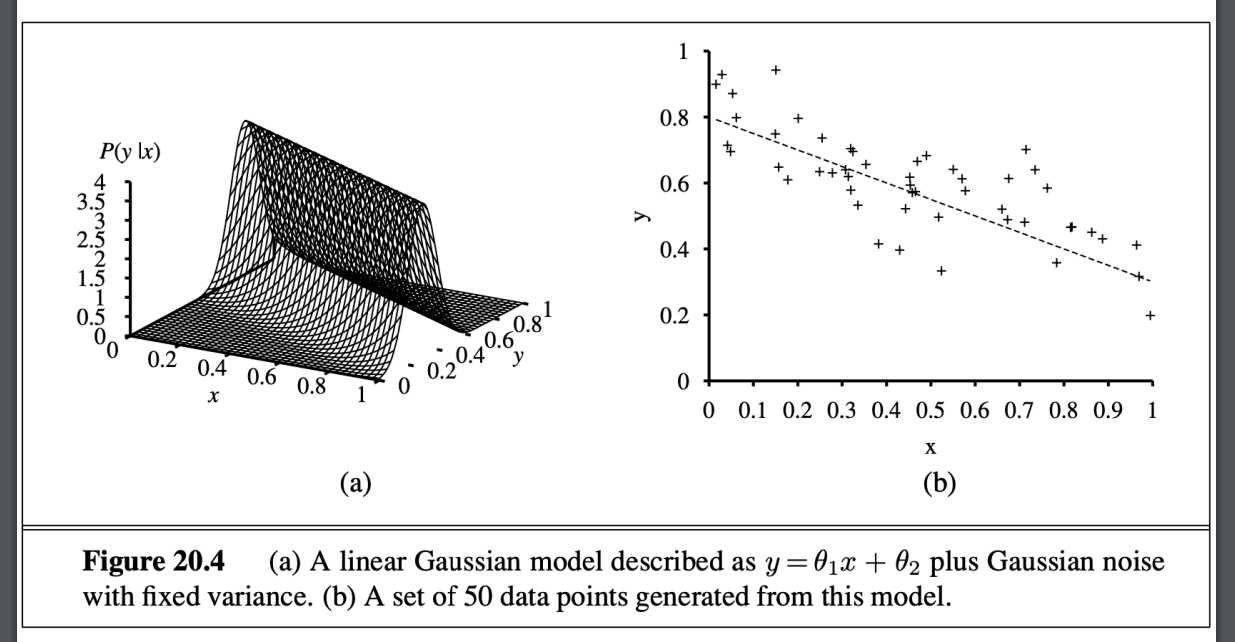
- 圖像

- 解其實就是最小化 minimizing the numerator
in the exponent of Equation (20.5). - 相當於線性回歸 解square error
- 圖像
Bayesian parameter learning
小數據集造成的問題

- Bayeisan 使用一個假設先驗 根據可能的分佈
- 這段話指出,當數據量不足時,單純依賴最大似然方法可能導致極端結論,而引入先驗知識的貝葉斯方法能更好地解決這一問題。這也反映了貝葉斯方法在參數學習中的核心優勢:結合數據與先驗知識,動態更新模型。
假設的先驗知識


- 一種beta函數 由兩個超參數決定的 值域介於0~1

- 微調超參數帶來的差異
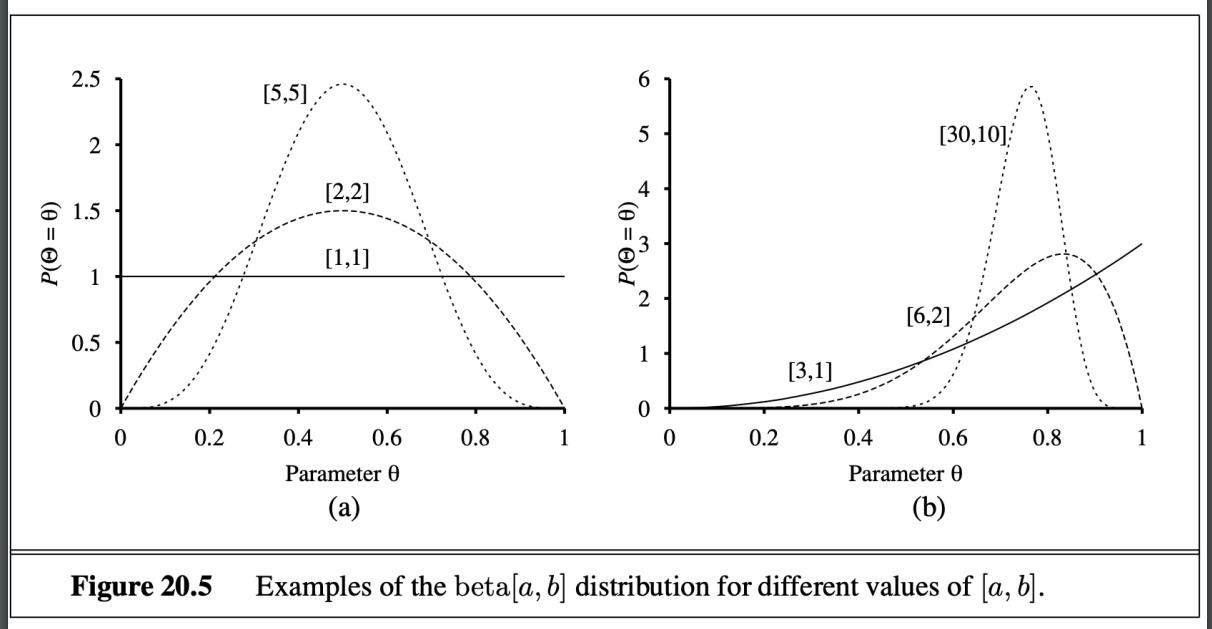
- 一種beta函數 由兩個超參數決定的 值域介於0~1
beta函數是閉運算

a,b 就像糖果的虛擬計數


- 對大資料集 bayesian parameter learning 會收斂到 ML leanring
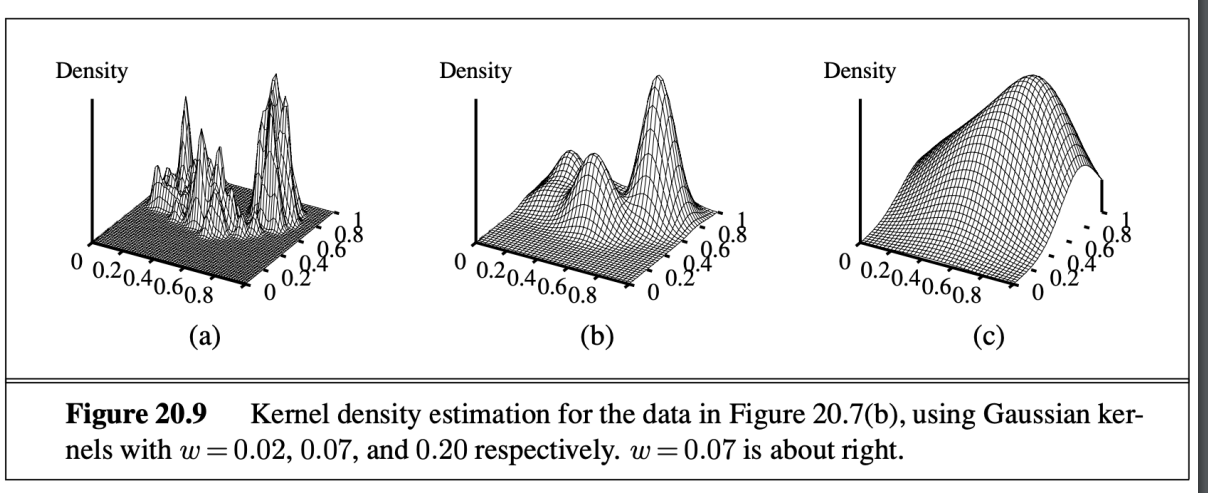
Density estimation with nonparametric models
能夠從樣本復原模型嗎?

- 非參數密度估計的概念
- 什麼是非參數密度估計?
- 非參數密度估計是一種估計概率分佈的方法,不需要事先對分佈的結構或參數化做任何假設。
- 這種方法主要適用於連續數據域,試圖直接從數據中學習概率密度函數 (PDF)。
- 為什麼叫非參數?
- 傳統的參數化方法,比如高斯分佈,假設數據分佈可以由幾個參數(如均值和標準差)完全描述。
- 非參數方法則不依賴具體的分佈假設,而是使用數據樣本直接估計分佈。
- 非參數密度估計的概念
KNN

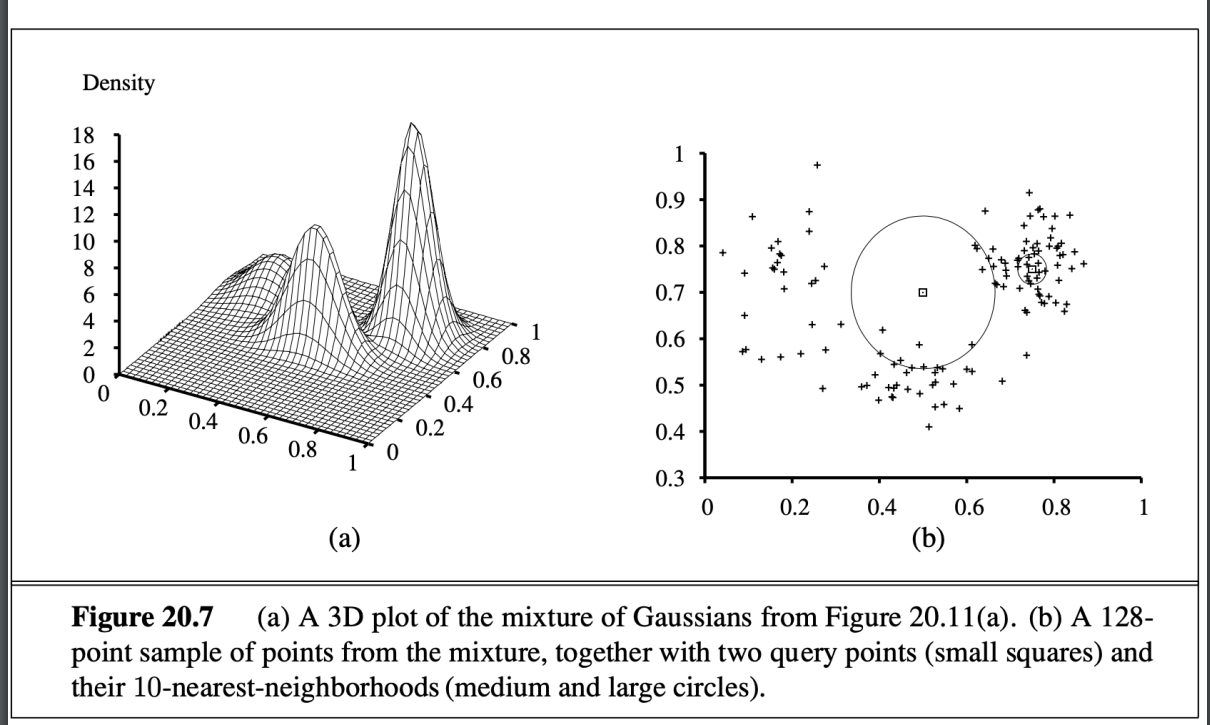
- 資料
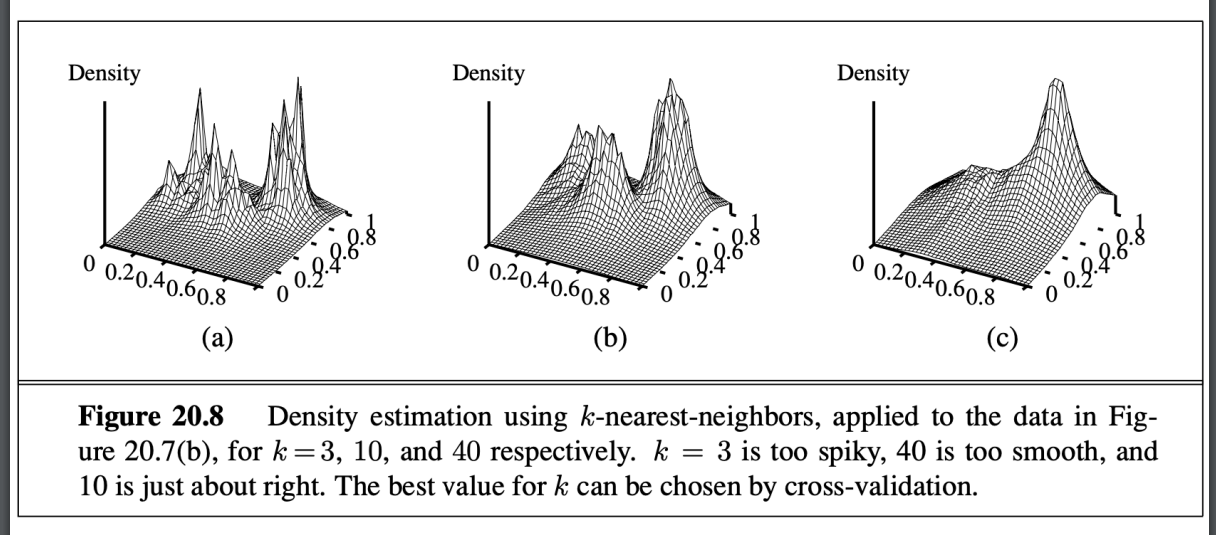
- 預測結果
- 資料
using kernal function

Learning with Hidden Variables: The EM Alg.
隱藏參數

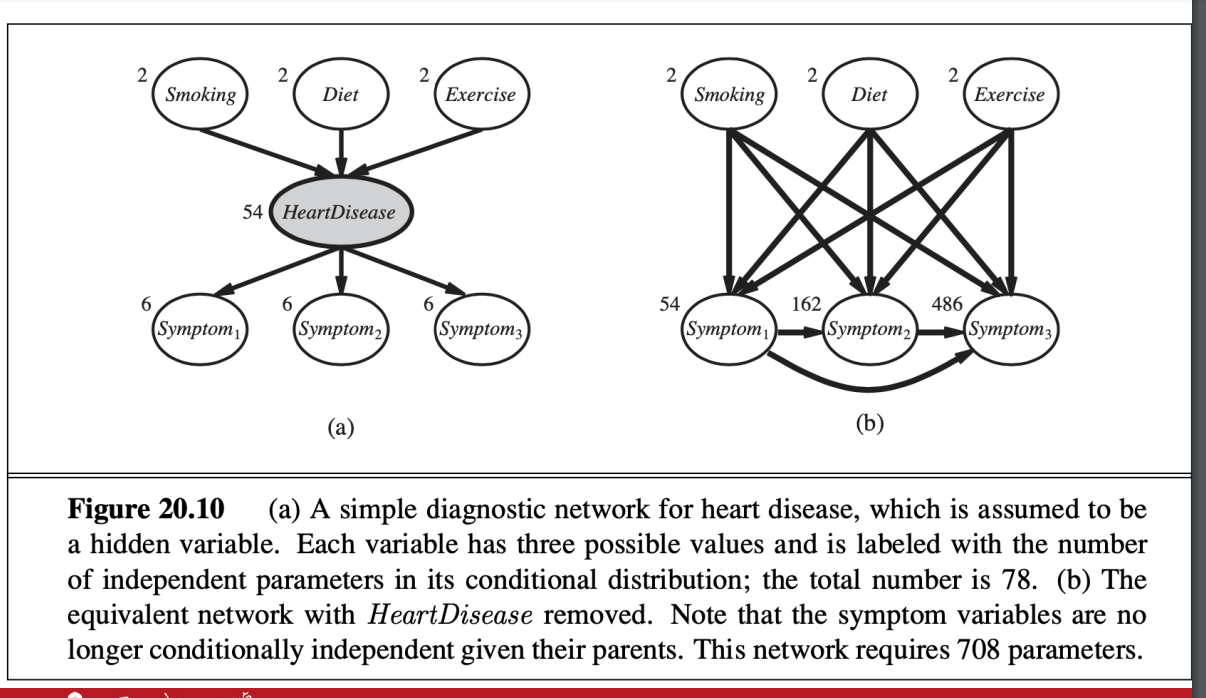
- 疾病本身不會被觀察到

- 隱藏參數本身可以簡化網路
- 疾病本身不會被觀察到
很難計算

- 使用EM (expectation maximization)
Unsupervised clustering: Learning mixtures of Gaussians
非監督式分群
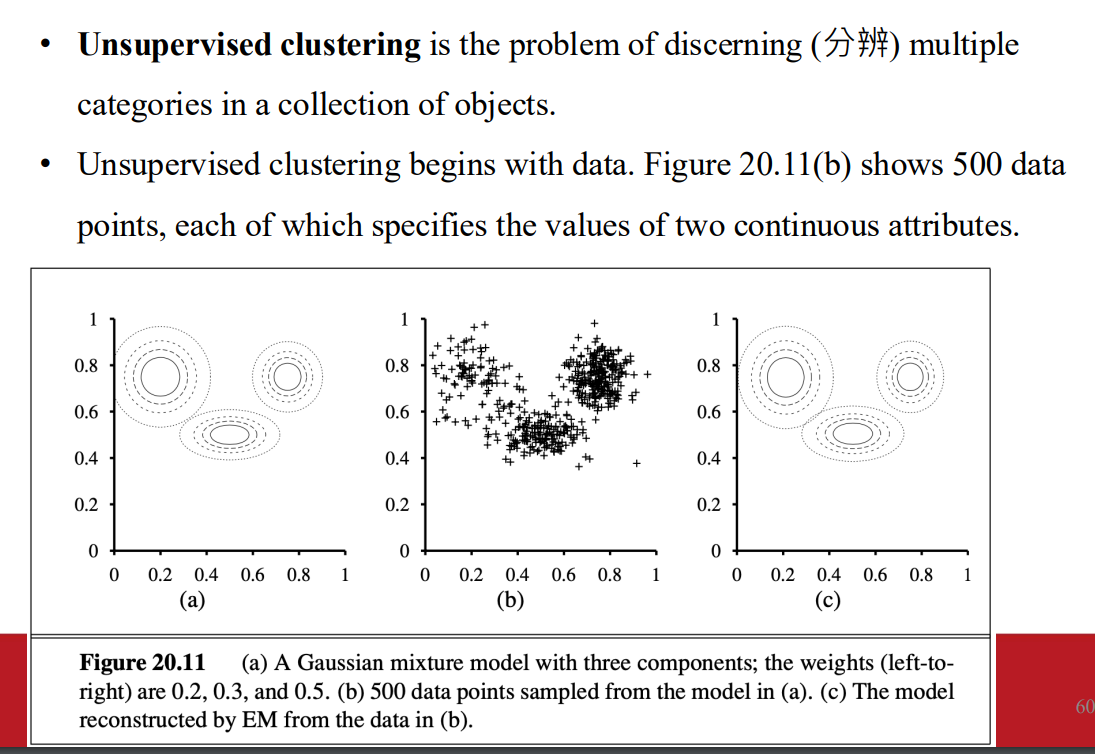
假設資料由混和分佈的 一個組件生成

- 高斯混合模型的背景
- 高斯混合模型是一種用來建模數據分佈的概率模型,它假設數據是由多個不同的高斯分佈(即分量 Gaussians)所組成。
- 在這種模型中,我們有:
- 多個高斯分佈(每個分佈有自己的均值和標準差)。
- 每個數據點來自某個高斯分佈(但我們不知道是哪一個)。
- 問題的目標是同時估計這些高斯分佈的參數(如均值、方差)和每個數據點的來源分量(即隱變量)。
- 高斯混合模型的背景
對於連續資料 一個自然的混和分佈選擇是高斯分布


- 問題是不知道參數以及標籤
EM

- 假設我們知道參數 並隨機分配資料點
- 每次根據資料點屬於該分佈的機率 去更新資料點的所屬分佈 直到收斂
E-step

M-step

解釋

- E-step 相當於計算隱藏的indicator variable
- M-step 更新參數
比較
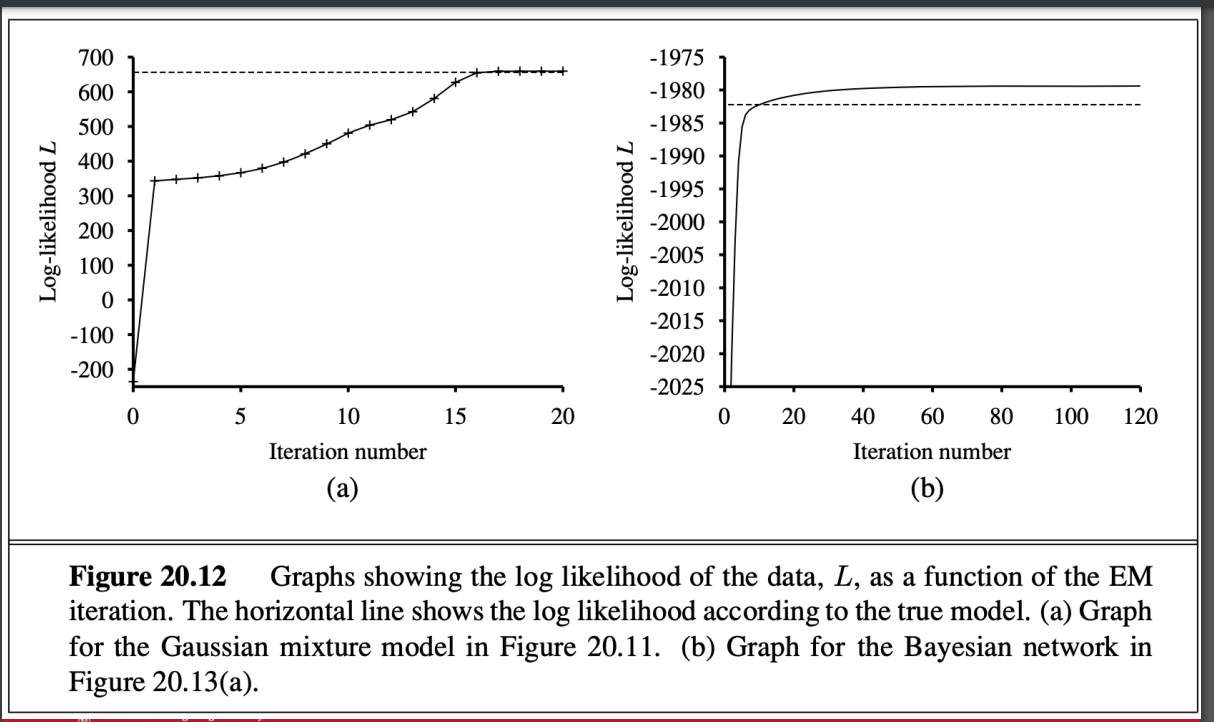
兩個特點

- 第一點:學到的模型的對數似然值 (Log Likelihood)
- 觀察:最終學到的模型的對數似然值略高於生成數據的原始模型。
- 原因:
- 數據是隨機生成的,可能並未完美反映原始模型的真實分佈。
- 因此,學到的模型能夠在特定的數據集上更好地「擬合」數據,導致對數似然值略高於原始模型的理論值。
- 這是一種過擬合的現象,因為模型過度擬合了特定數據集的特徵,而不一定能完美表現原始模型的全域分佈。
- 第二點:EM 演算法的特性
- 對數似然值的單調增加:
- EM 演算法在每次迭代中,都會增加數據的對數似然值。
- 這是因為 EM 保證每次更新後,模型對數似然值都不會降低(數學證明來自於 EM 的兩個步驟:期望步驟 (E-step) 和最大化步驟 (M-step) 的設計)。
- 局部最大值:
- 在特定條件下,EM 可以證明會達到對數似然的局部最大值。
- 這意味著演算法的最終結果可能依賴於初始參數值,而不一定是全局最大值。
- 與梯度上升法的類比:
- EM 的行為類似於一種基於梯度的爬山算法 (hill-climbing algorithm),因為它在對數似然的表面上「爬升」到更高的值。
- 但不同的是,EM 不需要「步長參數 (step size)」,因為它通過解析解(最大化步驟)直接找到每次迭代中的最佳更新。
- 對數似然值的單調增加:
- 第一點:學到的模型的對數似然值 (Log Likelihood)
Learning Bayesian networks with hidden variable
問題定義

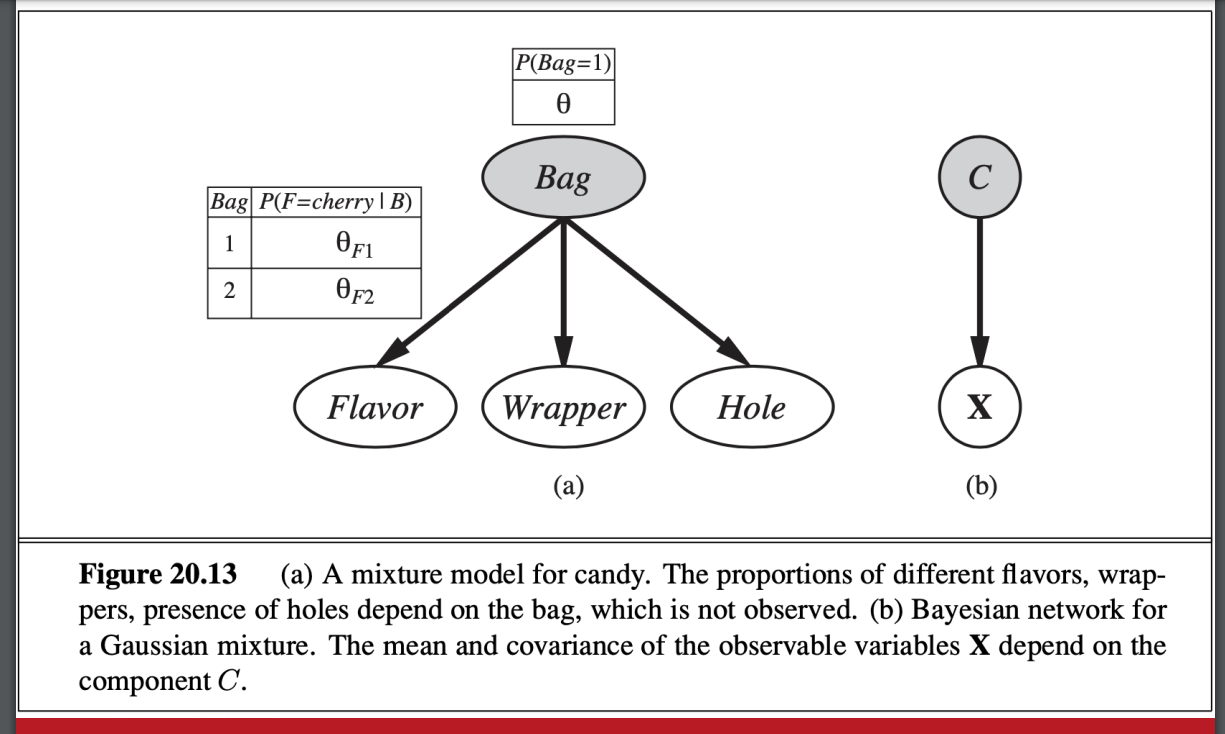
如果來自不同袋子的糖果被混和放進一個袋子


- 觀察到的樣本
E-step


- 得到

- 其他參數同理
- 得到
變化

- 學習最後階段都會混和其他 gradient-based method (Newton-raphson)
對於bayesian network 隱藏參數的學習
>
- 來自於推理的結果 只跟局部後驗機率有關
The general form of the EM algorithm
- 廣泛形式




- 各步解釋


- 用馬可夫鍊蒙地卡羅(MCMC)近似估計 E-step中的後驗機率
- 各步解釋
Chapter 20 Learning Probabilistic Models
https://z-hwa.github.io/webHome/[object Object]/Introduction to Artificial Intelligence/Chapter-20-Learning-Probabilistic-Models/