S6-Chap6-Basics of Digital Audio-2025
Chap6-Basics of Digital Audio
6.1 Digitization of Sound
聲音是什麼 (What is Sound?)

- 聲音是一種像光一樣的波動現象,但它是宏觀的,涉及空氣分子的壓縮和膨脹。
- 例如,音響系統中的揚聲器前後振動,產生我們感知為聲音的縱向壓力波。
- 由於聲音是壓力波,它具有連續值,而不是數位化的離散值

- 即使聲音是縱向壓力波,它仍然具有普通的波動特性和行為,例如反射(反彈)、折射(進入不同密度的介質時改變角度)和繞射(繞過障礙物彎曲)。
- 如果我們希望使用聲音波形的數位版本,我們必須形成音訊資訊的數位化表示。
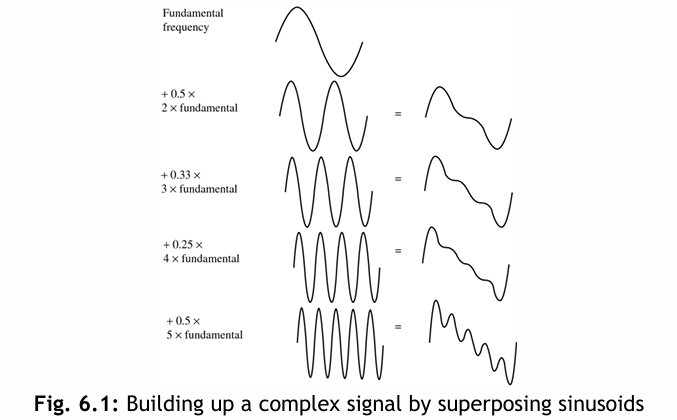
- 訊號可以分解為正弦波的總和。圖 6.1 展示了加權正弦波如何構成相當複雜的訊號。
音高、頻率、八度和諧波的概念

頻率是一個絕對的度量,而音高 (pitch) 通常是相對的 - 一種對聲音的主觀感知品質。
- (a) 音高和頻率 相關,例如中央 C 上方的 A 音被設定為精確的 440 Hz。
- (b) 八度 (octave) 是頻率翻倍的音程。比 440 Hz 的 A 高一個八度是 880 Hz。
- (c) 諧波 (harmonics) 是頻率為基音頻率整數倍的一系列樂音。
- (d) 如果允許非整數倍的基頻,就會有更多的泛音,聲音也會更複雜。
下方展示了一個鋼琴鍵盤,標註了從 A0 到 C8 的不同音符。
6.1.2 Digitization
- 數位化 (Digitization) 意味著轉換為數字流,並且為了效率,這些數字最好是整數。
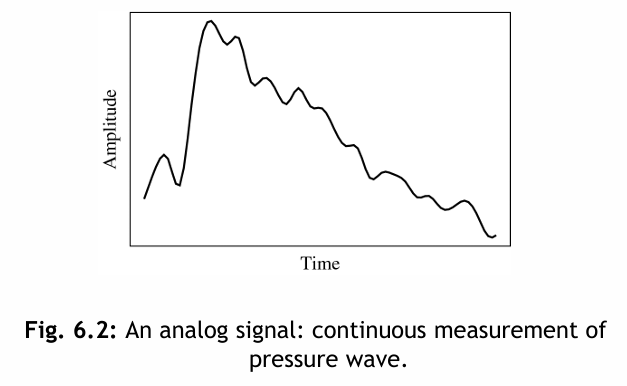
- 圖 6.2 顯示了聲音的一維特性:振幅值取決於一個一維變數,即時間。(注意,圖像的數值取決於二維變數,x 和 y)。
數位化的過程

包括取樣和量化:
為了數位化訊號,必須在每個維度上進行取樣 (sampled):時間和振幅。
- (a) 取樣 (Sampling) 意味著以通常均勻間隔測量我們感興趣的量。
- (b) 時間取樣 只是在均勻的時間間隔進行測量,其速率稱為取樣頻率 (sampling frequency)。
- (c) 音訊的典型取樣率 從 8 kHz 到 48 kHz。這個範圍由之後討論的奈奎斯特定理決定。
- (d) 振幅或電壓維度的取樣 稱為量化 (quantization)。
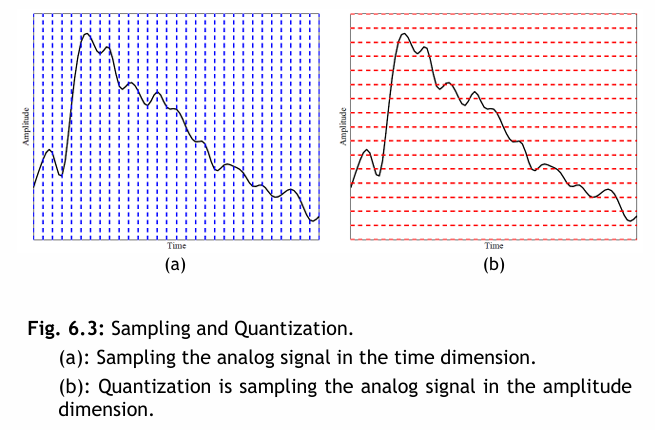
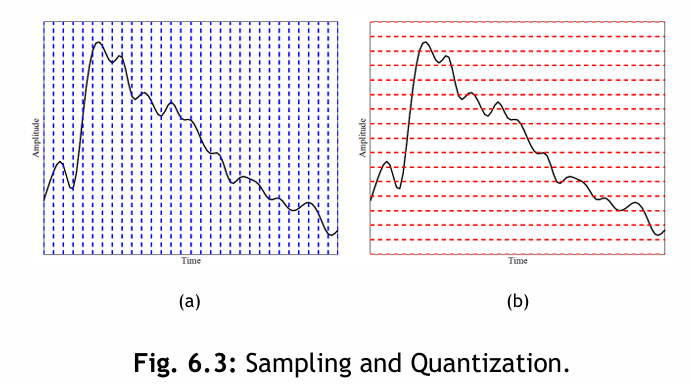
這張圖片展示了取樣和量化 (Sampling and Quantization):
(a) 時間取樣 (Sampling the analog signal in the time dimension): 圖 (a) 顯示了在時間維度上對類比訊號進行取樣。藍色的垂直虛線表示以均勻的時間間隔對連續的類比訊號(黑線)進行測量。
(b) 量化 (Quantization is sampling the analog signal in the amplitude dimension): 圖 (b) 顯示了在振幅維度上對類比訊號進行量化。紅色的水平虛線表示將連續的振幅值近似到離散的量化級別。類比訊號(黑線)的振幅被映射到最接近的紅色水平線。
如何數位化音訊數據需要回答的問題

- 取樣率是多少? (What is the sampling rate?)
- 數據的量化精細度如何?量化是均勻的嗎? (How finely is the data to be quantized, and is quantization uniform?)
- 音訊數據如何格式化?(檔案格式) (How is audio data formatted? (file format))
6.1.3 Nyquist Theorem
奈奎斯特定理 (Nyquist theorem)

奈奎斯特定理 (Nyquist theorem) 和取樣率對訊號重建的影響:
- 奈奎斯特定理 指出為了能夠恢復原始聲音,我們必須以多高的頻率在時間上進行取樣。
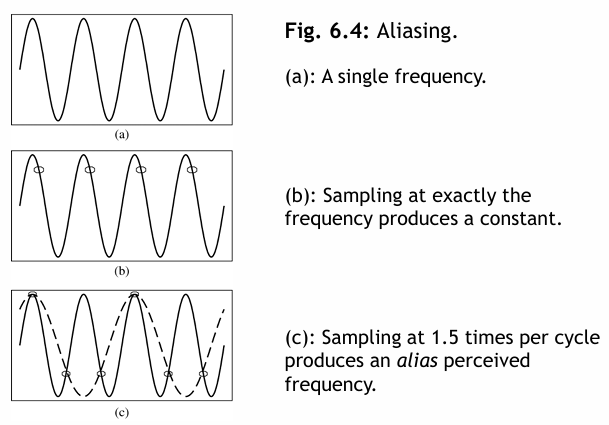
- (a) 圖 6.4(a) 顯示了一個單一的正弦波:它是一個單一的、純粹的頻率(只有電子樂器才能產生這樣的聲音)。
- (b) 如果取樣率恰好等於實際頻率,圖 6.4(b) 顯示檢測到一個錯誤的訊號:它只是一個常數,頻率為零。

- (a) 如果以實際頻率的 1.5 倍進行取樣,圖 6.4(c) 顯示我們得到一個錯誤的(混疊)頻率,它比正確的頻率低——它是正確頻率的一半(波長是實際訊號的兩倍)。
- (b) 因此,為了正確取樣,我們必須使用至少等於訊號中最高頻率成分兩倍的取樣率。這個速率稱為奈奎斯特速率 (Nyquist rate)。
總結

奈奎斯特定理和相關概念
正弦波的顯現頻率 (apparent frequency) 以及頻率摺疊 (frequency folding)
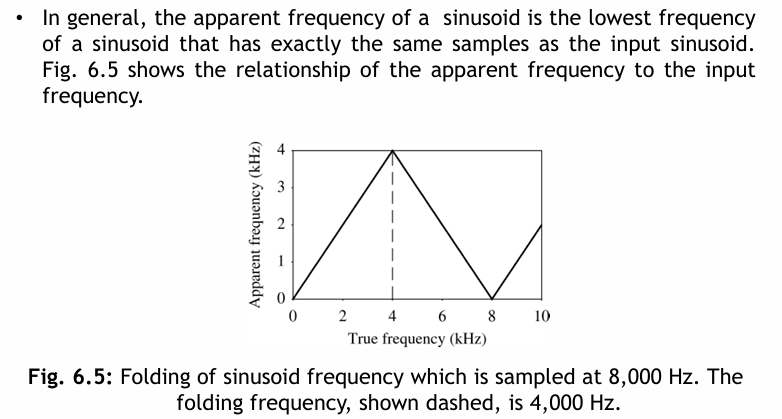
一般來說,正弦波的顯現頻率是具有與輸入正弦波完全相同的樣本的最低頻率的正弦波。圖 6.5 顯示了顯現頻率與輸入頻率的關係。
圖 6.5:以 8,000 Hz 取樣的正弦波頻率的摺疊。摺疊頻率(以虛線表示)為 4,000 Hz。
圖表顯示,當真實頻率從 0 Hz 增加到取樣頻率的一半(即奈奎斯特頻率,此處為 4,000 Hz)時,顯現頻率也線性增加。然而,當真實頻率超過奈奎斯特頻率時,顯現頻率會開始下降。當真實頻率達到取樣頻率時(8,000 Hz),顯現頻率又變回 0 Hz。之後,顯現頻率再次開始增加。這種現象稱為頻率摺疊,奈奎斯特頻率(取樣頻率的一半)也稱為摺疊頻率 (folding frequency)。
簡單來說,顯現頻率 就是我們實際聽到的頻率,它可能和原始聲音的真實頻率不一樣,特別是在數位化取樣的過程中。
頻率摺疊 就像一面鏡子,以奈奎斯特頻率(取樣頻率的一半)為中心。
- 當原始聲音的真實頻率 低於這個中心點時,我們數位化後聽到的 顯現頻率 和原始頻率是一樣的。
- 但是,當原始聲音的真實頻率 高於這個中心點時,數位化後聽到的 顯現頻率 就會「摺疊」回來,變成一個較低的頻率。而且原始頻率越高,摺疊回來的顯現頻率就越低,然後又開始升高。
圖表的意思是:
假設我們的數位化取樣率是 8000 Hz。那麼,摺疊頻率(中心點)就是 4000 Hz。
- 如果原始聲音的頻率是 1000 Hz,那麼我們聽到的也是 1000 Hz。
- 如果原始聲音的頻率是 3000 Hz,那麼我們聽到的也是 3000 Hz。
- 但是,如果原始聲音的頻率是 5000 Hz(高於 4000 Hz),那麼我們聽到的就會是 |8000 - 5000| = 3000 Hz。
- 如果原始聲音的頻率是 7000 Hz,那麼我們聽到的就會是 |8000 - 7000| = 1000 Hz。
- 如果原始聲音的頻率是 9000 Hz,那麼我們聽到的就會是 |8000 - 9000| = 1000 Hz。
這就是為什麼在數位化聲音時,如果取樣率不夠高,高頻的聲音就會被錯誤地表示成低頻的聲音,產生失真,也就是所謂的混疊 (aliasing)。這也是為什麼奈奎斯特定理要求取樣率至少是原始訊號最高頻率的兩倍,以避免這種頻率摺疊現象的發生。
6.1.4 Signal to Noise Ratio (SNR)

訊號雜訊比 (Signal to Noise Ratio, SNR)
訊號雜訊比 (SNR) 的範例

訊號雜訊比 (SNR) 的範例
周圍常見聲音的音量等級,以分貝 (dB) 為單位,並將其與人類聽覺的閾值進行比較:
我們周圍聽到的常見聲音的音量通常用分貝來描述,它是相對於我們能夠聽到的最安靜的聲音的比率。表 6.1 顯示了這些聲音的大約音量等級。
表 6.1:常見聲音的音量等級,以分貝為單位
| 聲音 | 分貝 (dB) |
|---|---|
| 聽覺閾值 | 0 |
| 樹葉的沙沙聲 | 10 |
| 非常安靜的房間 | 20 |
| 一般的房間 | 40 |
| 對話 | 60 |
| 繁忙的街道 | 70 |
| 大聲的收音機 | 80 |
| 火車通過車站 | 90 |
| 鉚釘槍 | 100 |
| 不適閾值 | 120 |
| 疼痛閾值 | 140 |
| 損害耳膜 | 160 |
這個表格展示了不同環境和聲音的相對響度,從幾乎聽不見的聲音到可能引起不適或損害聽力的聲音。
6.1.5 Signal to Quantization Noise Ratio (SQNR)

量化雜訊 (quantization noise)
訊號對量化雜訊比 (Signal to Quantization Noise Ratio, SQNR)




6.1.6 Linear and Non-linear Quantization
線性格式和非均勻量化的概念

解

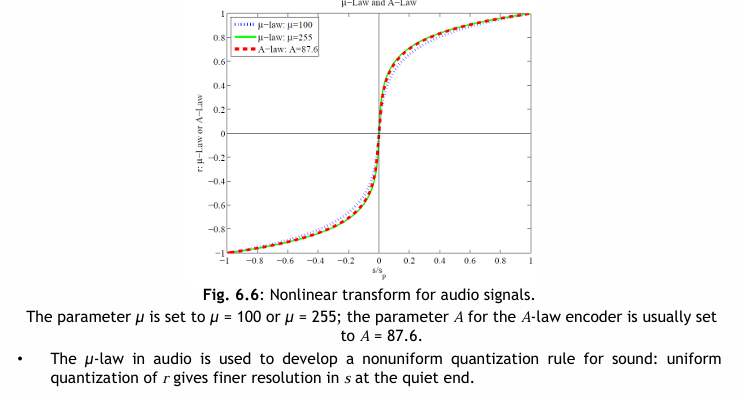
μ-law 的位元分配 (Bit allocation) 策略

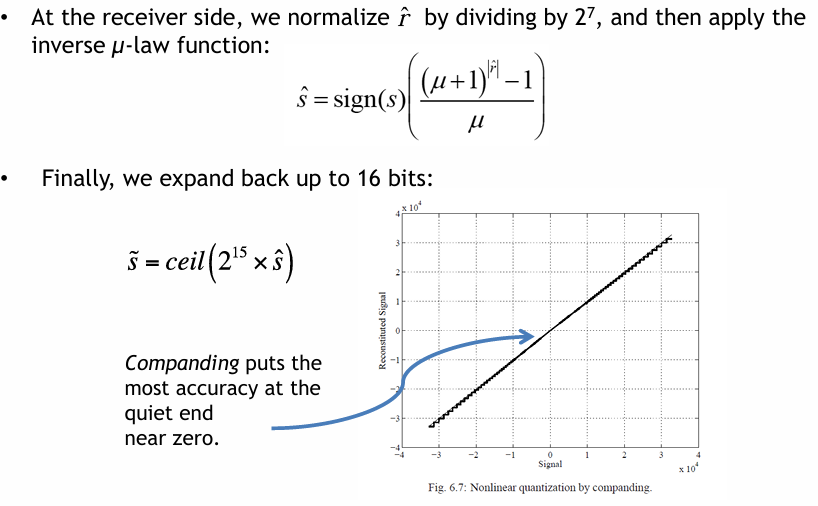
μ-law 在接收端的解碼過程,以及最終的位元擴展
6.1.7 Audio Filtering
濾波 (filtering) 處理

6.1.8 Audio Quality vs. Data Rate
數位音訊傳輸的數據速率和頻寬需求

為了傳輸數位音訊訊號,隨著量化使用的位元數增加,未壓縮的數據速率也會增加。立體聲 (Stereo) 傳輸則需要雙倍的頻寬,因為需要傳輸兩個獨立的聲道。
表 6.2:常見音訊應用中的位元率和頻寬
| 品質 | 取樣率 (kHz) | 每樣本位元數 | 單聲道/立體聲 | 位元率 (未壓縮) (kB/sec) | 訊號頻寬 (Hz) |
|---|---|---|---|---|---|
| 電話 | 8 | 8 | 單聲道 | 8 | 200-3,400 |
| AM 收音機 | 11.025 | 8 | 單聲道 | 11.0 | 100-5,500 |
| FM 收音機 | 22.05 | 16 | 立體聲 | 88.2 | 20-11,000 |
| CD | 44.1 | 16 | 立體聲 | 176.4 | 5-20,000 |
| DVD 音訊 | 192 (最大) | 24 (最大) | 高達 6 聲道 | 1,200.0 (最大) | 0-96,000 (最大) |
這個表格展示了不同音訊品質的應用所需的取樣率、量化位元數、聲道數以及由此產生的未壓縮位元率和訊號頻寬。可以看出,更高品質的音訊需要更高的取樣率和位元深度,從而導致更高的數據速率和頻寬需求。立體聲傳輸的位元率是單聲道的兩倍。
6.3 Quantization and Transmission of Audio
音訊編碼 (Coding of Audio)


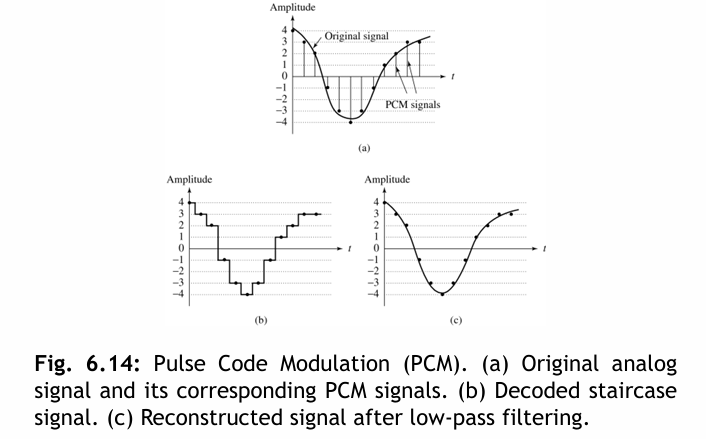
6.3.2 Pulse Code Modulation


每個壓縮方案 (compression scheme) 通常包含的三個階段


PCM in Speech Compression

需要處理的兩個細節


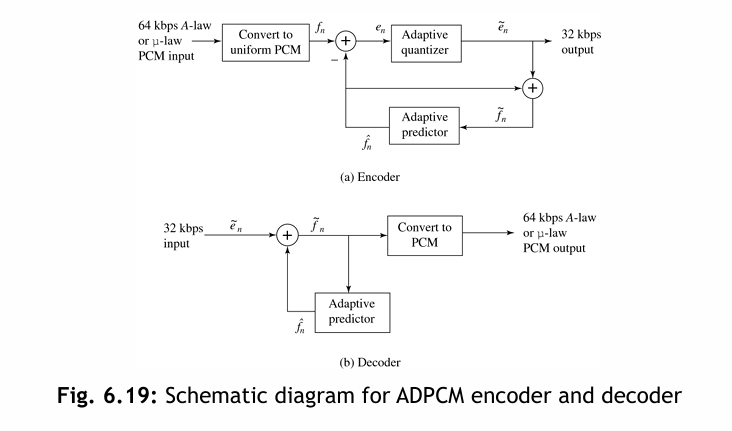
轉換流程圖
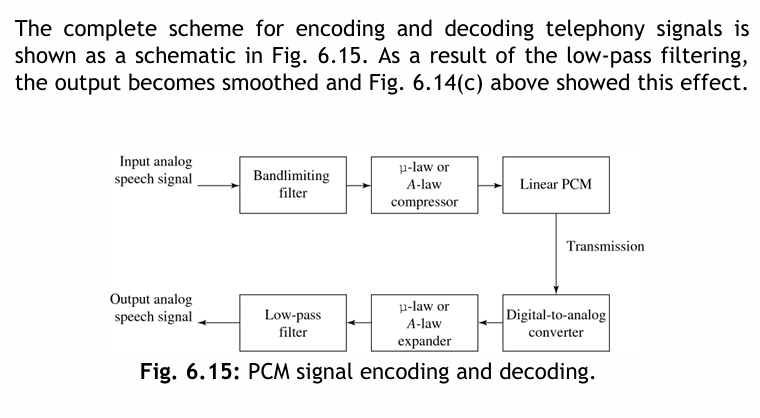
6.3.3 Differential Coding of Audio


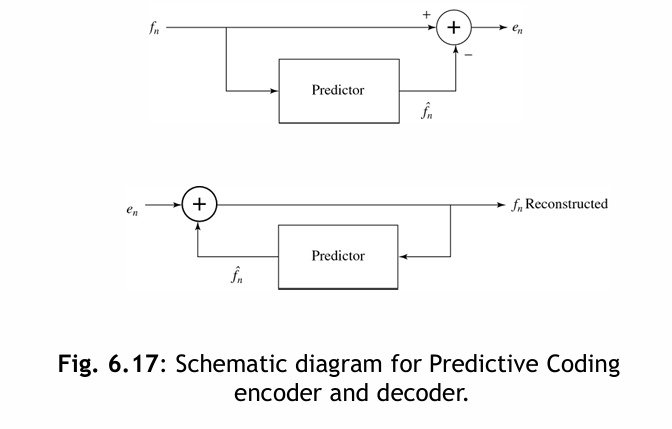
6.3.4 Lossless Predictive Coding

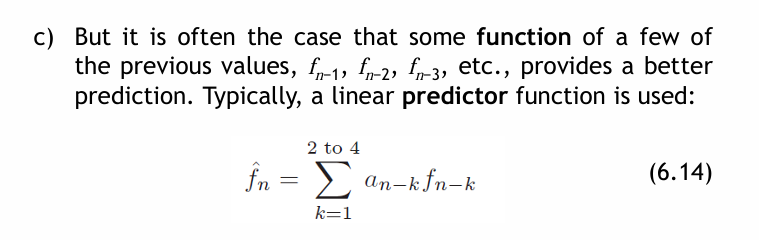
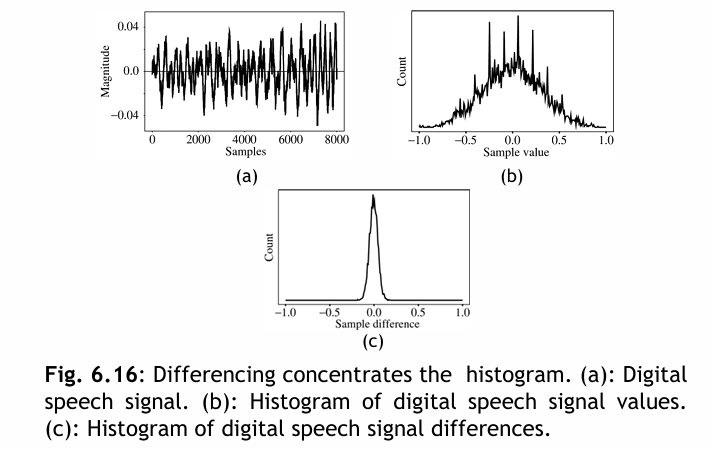
形成差異以提高壓縮效率的原理

差分編碼可能帶來的一個問題以及一種解決方案

簡單的預測器範例

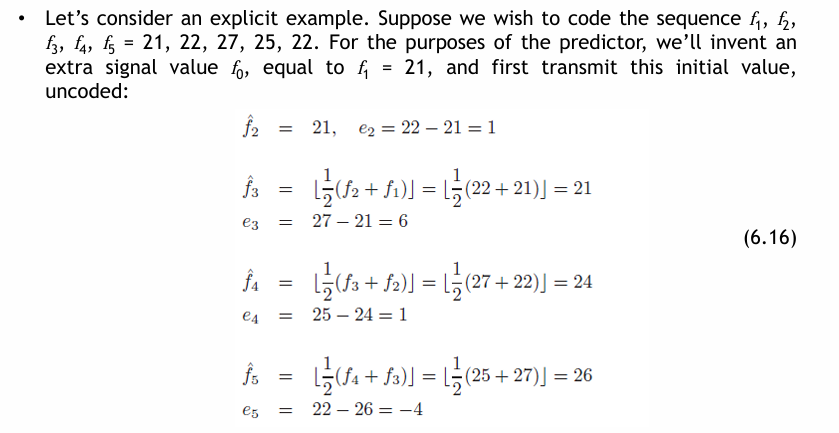

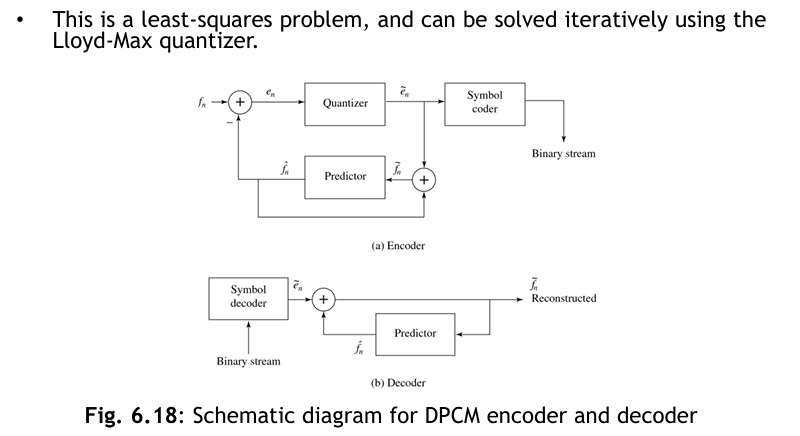
6.3.5 DPCM

自適應量化 (adaptive quantization) 的概念

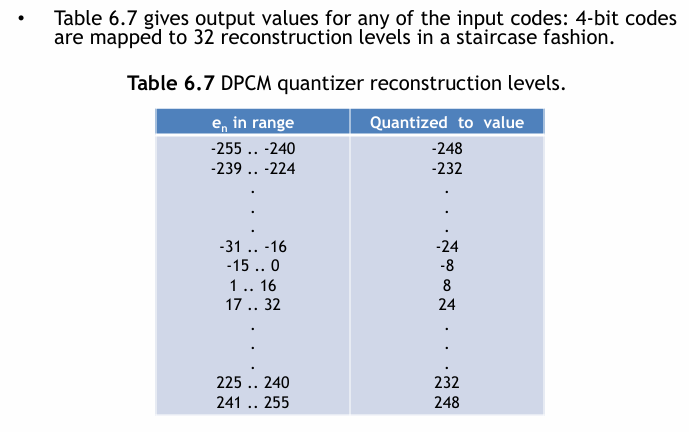
DPCM 系統中量化器的具體實現

DPCM 範例

6.3.6 DM



6.3.7 ADPCM